Problema nº 4 de trigonometría, funciones trigonométricas - TP03
Enunciado del ejercicio nº 4
Hallar los valores sin emplear la calculadora:
a) sen 240° =
b) tg 225° =
c) tg 300° =
e) sen 390° =
f) sec 135° =
g) sec 660° =
Recordamos la tabla de valores:
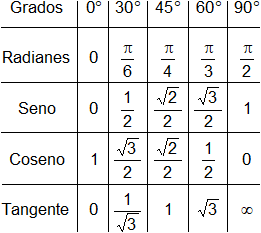
Los signos de las funciones en los distintos cuadrantes:

Solución
a)
El ángulo está en el cuadrante III:
sen 240° = sen (240° - 180°) = -sen 60° =
Reemplazamos por los valores de la tabla:
![]()
b)
El ángulo está en el cuadrante III:
tg 225° = tg (225° - 180°) = tg 45° =
Reemplazamos por los valores de la tabla:
tg 225° = tg 45° = 1
c)
El ángulo está en el cuadrante IV:
![]()
d)
El ángulo tiene más de un giro, dividimos por 360°:
390°/360° = 1,08
Le restamos 1 giro:
390° - 360° = 30°
El ángulo está en el cuadrante I:
sen 390° = sen 30° = ½
e)
El ángulo está en el cuadrante II:
sec 135° = sec (180° - 135°) = sec 45° =
Sabemos que:
![]()
![]()
Reemplazamos por los valores de la tabla:
![]()
Racionalizamos el denominador:
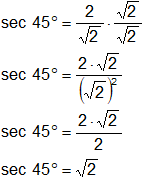
f)
El ángulo tiene más de un giro, dividimos por 360°:
660°/360° = 1,8
Le restamos 1 giro:
660° - 360° = 300°
El ángulo está en el cuadrante IV:
sec 660° = sec 300° = sec (300° - 360°) = sec -60° = sec 60°
Sabemos que:
![]()
![]()
Reemplazamos por los valores de la tabla:
![]()
sec 660° = 2
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo, cómo calcular funciones trigonométricas