Problema nº 4 de sistemas angulares, interpretar funciones trigonométricas - TP04
Enunciado del ejercicio nº 4
Dibujar en cada caso el ángulo correspondiente:
a) Un ángulo agudo cuyo seno sea ¾.
b) Un ángulo obtuso cuyo coseno sea -½.
c) Un ángulo cualquiera cuya tangente sea 1,5.
d) Un ángulo cualquiera cuyo coseno sea 3/2.
e) Un ángulo obtuso cuya secante sea -1,5.
f) Los ángulos comprendidos entre 0 y 2·π, cuyo coseno sea ⅔.
Los signos de las funciones en los distintos cuadrantes:
| I | II | III | IV | |
| sen / cosec | + | + | - | - |
| cos / sec | + | - | - | + |
| tg / cotg | + | - | + | - |
Solución
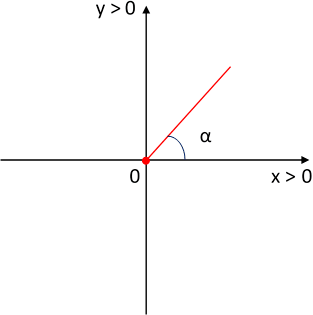
a)
Un ángulo agudo cuyo seno sea ¾.
Se plantea la función trigonométrica inversa para hallar el ángulo:
α = arcsen ¾
0 ≤ α ≤ 90° ⟶ agudo
α = 0,848062079 rad
Lo pasamos a grados grados sexagesimales con dos decimales:
180° = π rad
| π rad | ⟶ | 180° |
| 0,848062079 rad | ⟶ | α |
| α = | 0,848062079 rad·180° |
| π rad |
α = 48,59° ⟶ agudo
b)
Un ángulo obtuso cuyo coseno sea -½.
Se plantea la función trigonométrica inversa para hallar el ángulo:
α = arccos -½
90° ≤ α ≤ 180° ⟶ obtuso
α = 2,094395102 rad
Lo pasamos a grados grados sexagesimales con dos decimales:
180° = π rad
| π rad | ⟶ | 180° |
| 2,094395102 rad | ⟶ | α |
| α = | 2,094395102 rad·180° |
| π rad |
α = 120° ⟶ obtuso
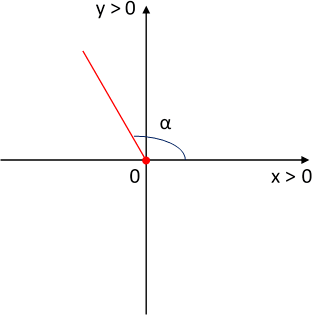
c)
Un ángulo cualquiera cuya tangente sea 1,5.
Se plantea la función trigonométrica inversa para hallar el ángulo:
α = arctg 1,5
α = 0,982793723 rad
Lo pasamos a grados grados sexagesimales con dos decimales:
180° = π rad
| π rad | ⟶ | 180° |
| 0,982793723 rad | ⟶ | α |
| α = | 0,982793723 rad·180° |
| π rad |
α = 56,31°
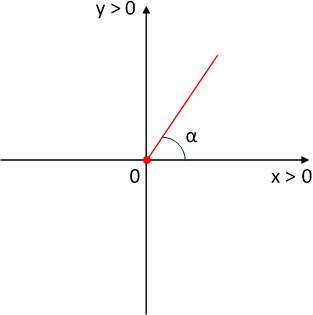
d)
Un ángulo cualquiera cuyo coseno sea 3/2.
El valor absoluto del coseno de cualquier ángulo da valores entre 0 y 1, por lo tanto, no existe el ángulo.
0 ≤ |cos α| ≤ 1
e)
Un ángulo obtuso cuya secante sea -1,5.
Se plantea la función trigonométrica inversa para hallar el ángulo:
sec α = -1,5
| sec α = | 1 |
| cos α |
| cos α = | 1 |
| sec α |
| cos α = | 1 |
| -1,5 |
cos α = -0,667
α = arccos -0,667
90° ≤ α ≤ 180° ⟶ obtuso
α = 2,300523983
Lo pasamos a grados grados sexagesimales con dos decimales:
180° = π rad
| π rad | ⟶ | 180° |
| 2,300523983 rad | ⟶ | α |
| α = | 2,300523983 rad·180° |
| π rad |
α = 131,81° ⟶ obtuso
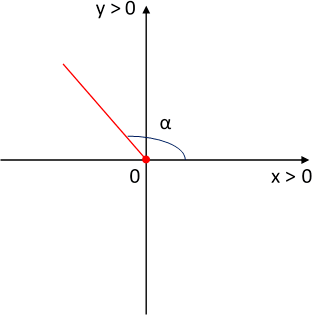
f)
Los ángulos comprendidos entre 0 y 2·π, cuyo coseno sea ⅔.
Se plantea la función trigonométrica inversa para hallar el ángulo:
α = arccos ⅔
El coseno es positivo en los cuadrantes I y IV.
α = 0,841068671
Lo pasamos a grados grados sexagesimales con dos decimales:
180° = π rad
| π rad | ⟶ | 180° |
| 0,841068671 rad | ⟶ | α |
| α = | 0,841068671 rad·180° |
| π rad |
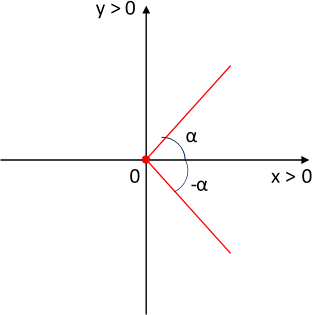
α = ±48,19°
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, cómo interpretar funciones trigonométricas