Ecuación de Arrhenius (primera parte)
La expresión de Svante August Arrhenius se obtuvo originalmente a partir de consideraciones termodinámica. Para una reacción elemental cuyas velocidades sean suficientemente rápidas y así alcanzar un equilibrio dinámico, la ecuación de Jacobus Henricus Van't Hoff enuncia que:
δ·ln K/dt = ΔH°·Rg·T²
Suponiéndose que la reacción es de la siguiente forma.
![]()
Con k₁ y k₂ siendo las constantes de velocidad directa e inversa. Las constantes de equilibrio y de velocidad se relacionan entre si por medio de la expresión:
K = K₂/K₁
Utilizando el resultado de la ecuación (1) se obtiene:
| d(ln k₂) | - | d(ln k1') | = | ΔH |
| dT | dT | RgT² |
La parte derecha de la ecuación (4) se puede dividir entre los cambios de entalpía, ΔH₁ y ΔH₂, de tal forma que:
ΔH = ΔH₂ - ΔH₁
Entonces la ecuación (5) puede separarse en forma de dos ecuaciones, una para la reacción directa y la otra para la inversa.
| d(ln k₂) | = | ΔH₂ |
| dT | RgT² |
| d(ln k1') | = | ΔH₁ |
| dT | RgT² |
Integrando cualquiera de las dos ecuaciones y haciendo que la constante de integración sea igual a ln A, se obtiene un resultado en forma de la ecuación de Arrhenius.
K = A·eΔH/Rg·T
Cabe mencionar que el procedimiento para obtener la ecuación de Arrhenius es muy similar.
Hablando estrictamente la ecuación de Arrhenius, está limitada a un proceso elemental, pues la ecuación de Arrhenius impone esta restricción. Sin embargo, el efecto exponencial de la temperatura suele representar con bastante precisión los datos de velocidad experimental para una reacción total, incluso cuando la energía de activación no este definida muy claramente y pueda ser una combinación de valores de E para diversas etapas elementales.
K = A·eΔH/Rg·T
La relación entre k y la temperatura para un proceso elemental obedece la ecuación de Arrhenius.
Reacción en cadena
Se ha demostrado que varios tipos importantes de reacciones industriales, tales como el cracking de hidrocarburos y la fotocloración, consisten en una serie de etapas elementales en las que hay uno o más intermediarios activos que se están regenerando continuamente. Estas regeneraciones hacen que los sistemas de este tipo sean especiales.
La primera etapa de una reacción en cadena es la formación de un intermediario activo, que puede ser un átomo o un radical libre. Puesto que este proceso requiere la ruptura de un enlace de una molécula estable, generalmente se necesita una energía considerable. Como resultado la energía de activación es alta y la velocidad en la etapa de iniciación es baja.
Para incrementar la velocidad de iniciación se puede aumentar la temperatura o usar una fuente externa de energía, tal como la energía radiante (iniciación fotoquímica). La iniciación va seguida de las etapas de propagación en las que se forma el producto y se regenera el átomo o el radical libre. Las velocidades de las etapas de propagación suelen ser altas, pues participan átomos o radicales libres muy reactivos. La energía de activación de estos procesos es baja.
La velocidad de formación del producto puede ser muy alta aun cuando la de iniciación sea baja. Esto se debe a que, una vez que se genera un átomo o un radical libre, éste puede producir muchas moléculas del producto estable por medio de las etapas de propagación suelen ser altas, pues participan átomos o radicales libres muy reactivos. La energía de activación de estos procesos es baja. La velocidad de formación del producto puede ser muy alta aun cuando la de iniciación sea baja. esto se debe a que, una vez que se genera un átomo o un radical libre, éste puede producir muchas moléculas del producto estable por medio de las etapas de propagación.
| Cl + W | k₆ | Producto final | Heterogéneas |
| ⟶ | |||
| Pr + W | k₇ | Producto final | |
| ⟶ | |||
Puede ser muy alta aun cuando la de iniciación sea baja. esto se debe a que, una vez que se genera un átomo o un radical libre, éste puede producir muchas moléculas del producto estable por medio de las etapas de propagación.
Esto es causado por la necesidad de eliminar pequeñas cantidades de sustancias que actúan para eliminar radicales libres o átomos. La velocidad será de cero durante el período de tiempo en el que estas sustancias, que casi siempre son impurezas como el oxígeno, se consumen para producir radicales libres.
Otra de las evidencias de un mecanismo en cadena es la existencia de velocidades muy altas (por ejemplo las explosivas) cuando se generan dos ó más radicales libres por cada radical consumido. La velocidad en cadena está limitada por la extracción del intermediario activo en la tercera etapa del mecanismo "Reacciones de terminación". Los tres tipos de etapas elementales (iniciación, propagación terminación), determinan la velocidad neta de formación de productos. Puesto que los átomos o radicales libres son muy reactivos, la hipótesis del estado estacionario, resulta una buena aproximación.
Considerando como ejemplo la cloración del propano (Pr H). La experiencia en laboratorio sugiere la siguiente secuencia:
| Cl₂ | ⟶ | 2·Cl | Propagación |
| Cl + PrH | k₂ | Pr + HCl | Terminación |
| ⟶ | |||
| Cl + Cl | k₄ | Cl₂ | Homogéneas |
| ⟶ | |||
| Cl + Pr | k₅ | PrCl | |
| ⟶ | |||
Iniciación
En la etapa de iniciación, los átomos de cloro activados pueden obtenerse por medio de colisiones intermoleculares de moléculas calentadas a temperaturas elevadas. Por otra parte, la molécula de cloro puede absorber energía radiante de la longitud de onda apropiada para disociarse.
Las etapas de propagación son por lo general reacciones que forman productos. Solamente se necesita una pequeña cantidad de iniciación para empezar la cadena y lograr velocidades altas de formación de productos. Solo se requiere una pequeña cantidad de iniciación para iniciar la cadena y obtenerse grandes velocidades de formación de productos.
En el caso de la polimerización esta no se verifica por medio de una secuencia normal de reacciones en cadena, pues no se regenera el reactante activado, no existe un portador de cadena. Sin embargo, el proceso total puede analizarse en muchos casos como una combinación de etapas de iniciación, propagación y terminación.
Efecto salino primario (Reacciones iónicas)
La mayoría de las reacciones entre los iones en solución, particularmente entre iones simples de carga opuesta, se producen tan rápidamente que hasta hace poco era imposible medir las velocidades de estas reacciones.
Hay algunas reacciones entre iones y moléculas neutrales que se desarrollan tan lentamente que permiten el empleo de métodos ordinarios. Las constantes de velocidad de estas reacciones dependen de la intensidad iónica de la solución.
La ecuación k = k₀·((γA·γB)/γ°), fue deducida primero por Johannes Nicolaus Brønsted y Bjerrum, antes de que se expusiera la teoría de las velocidades absolutas de reacción: si se aplica a las reacciones iónicas.
Al combinar esta ecuación con la ley límite para coeficientes de actividad iónica de Debye-Hückel, puede deducirse la dependencia de la constante de velocidad con la intensidad iónica. Al expresa la ecuación anterior en forma logarítmica.
log₁₀ k = log₁₀ k₀ + log₁₀ γA + log₁₀ γB - log₁₀ γ# (1)
Para un ion simple se encuentra, que la ley límite de Debye-Hückel es:
log₁₀ i = -A·z·i₂·(μ)½ (2)
Donde A es una constante; en agua a 25 °C, A = 0,50, aplicando la ley límite en la ecuación (1), sabiendo que z# = zA + zB, se transforma en:
log₁₀ k = log₁₀ k₀ - A·[zA² + zB² - (zA + zB)²]·(μ)½ = log₁₀ k₀ + 2·A·zA·zB·(μ)½ (3)
Como A = 0,50 tenemos
log₁₀ k = log₁₀ k₀ + zA·zB·(μ)½ (4)
La gráfica de log 10·k contra la raíz cuadrada de la intensidad iónica nos daría, en solución diluida, una línea recta con una pendiente igual a zA·zB
Si los iones tienen signos iguales zA·zB es positivo y la constante de velocidad aumenta con el aumento de la intensidad iónica, Si tienen carga opuesta, la constante de velocidad disminuye con el aumento de la intensidad iónica. La ecuación (4) es una descripción del efecto salino cinético primario.
La siguiente figura indica la verificación de esta ecuación según LaMer. El acuerdo es realmente satisfactorio las reacciones para dicha figura son:
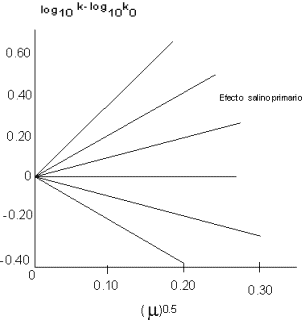
I. CO(NH₃)₅Br₂ + Hg²⁺, zA·zB = 4
II. S₂O₈⁼ + I⁻, zA·zB = 2
III. NO₂NCO₂C₂H₅⁻ + I⁻, zA·zB = 1
IV. C₁₂H₂₂ O₁₁ + OH⁻, zA·zB = 0
V. H₂O₂ + H⁺ + Br⁻, zA·zB = -1
VI. Co(NH₃)₅Br²⁺ + OH⁻, zA·zB = -2
La razón física tras el comportamiento en los casos de cargas iguales y desiguales en los iones, es resultado de la carga neta relativa en el complejo. El valor del coeficiente de actividad disminuye exponencialmente con z². Si ambos iones tiene el mismo signo, el complejo tiene una carga neta alta comparada con cualquier otra.
Ecuación de Eyring
El postulado fundamental de las teoría de las velocidades absolutas de reacción es el de que los reaccionantes se encuentran siempre en equilibrio con complejos activados. El complejo activado es aquella configuración de átomos que corresponden energéticamente a la cima de la barrera de energía que separa los reaccionantes y los productos. El equilibrio se expresa como
A + B _____ M
y la constante de equilibrio
K# = C#/CA·CB (2)
La concentración de los complejos activados es
C# = K#·CA·CB (3)
Conociendo la concentración de los complejos activados. el problema se reduce al calculo de la velocidad a la cual estos complejos se descomponen en productos; esto es se tiene que calcular la velocidad de reacción.
M# = Productos (4)
El complejo activado es un agregado de átomos que puede concebirse como similar a una molécula ordinaria, excepto que tiene una vibración especial respecto a la cual es inestable. Esta vibración conduce a la disociación del complejo en productos.
Si la frecuencia de esta vibración es v, entonces la velocidad a la cual se forman los productos es
velocidad = v·c# (moléculas/cm³·s) (5)
Pero la reacción elemental, A + B = Productos, tiene la velocidad
velocidad = k·cA·cB (6)
Al comparar las ecuaciones 5 y 6 encontramos que la constante de velocidad está dada por
k = v·K# (7)
Una revisión de las etapas envueltas en la deducción de la ecuación (7) muestra que está no depende de la sección de los dos reactantes, sino que es correcta para cualquier reacción elemental.
Pueden calcularse los valores de v y K# si expresamos la constante de equilibrio en términos de las funciones de partición molecular por unidad de volumen, f', entonces.
K# = f'#/fA·f'B (8)
Cualquier función de partición molecular puede expresarse en la forma f' = f·e⁻εo/kT la función f es la función de partición evaluada al aplicar energías relativas a la energía ε₀ de punto cero de la molécula. Por tanto, la ecuación se transforma en:
f# = f·v·f#. (9)
Donde f# es el remanente de f# después de que f·v ha sido factorizado. Si la frecuencia de esta vibración es v, entonces según quedaría:
f·v = k·T/hv·(e⁻hv/2·k·T) (10)
Si v es pequeño y hv/k·T menor a 1 como el exponente es casi igual a la unidad, f·v = k·T/hv y la ecuación (10)
f# = k·T/hv·f#(11)
Aplicando el valor de f# en la ecuación (9) obtenemos
K# = k·T/hv·(f#/fA·fB)·(e⁻Eo/RT) (12)
Definimos K# = f#/fA·fB)·e⁻Eo/RT) (13)
Entonces K# = (k·T/hv)·K# Usando este valor en la ecuación (7) obtenemos para la constante de velocidad.
K = k·T/h·(K#) Que es la ecuación de EYRING para la constante de velocidad de una reacción.
Bibliografía:
- Cinética de reacciones, Keith J. Laidler, Editorial Alhambra, Méxco D.F. 1979.
- Ingenieria de la Cinética Química, M. Smith, Editorial Continental, Méxco 1990.
- Fisícoquimica, Castellan W., Editorial M.H, Méxco 1991.
Autor: Cesar Arizmendi.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›