Guía nº 2 de ejercicios de cinética química
Resolver los siguientes ejercicios
Problema nº 1
En la tabla siguiente se dan las velocidades de reacción de A y B para diversas concentraciones de ambas especies. Dedúzcanse y la constante de velocidad k correspondiente a la reacción cinética:
v = k·[A]·[B]
| Experimento | [A] 10⁴ M | [B] 10⁵ M | v (m/s) |
| 1 2 3 | 2,3 4,6 9,2 | 3,1 6,2 6,2 | 5,2·10⁻⁴ 4,6·10⁻³ 1,664·10⁻² |
| v₃ | = | [A₃] |
| v₂ | [A₂] |
"k" no varía porque no varía ni la temperatura ni la naturaleza de los reactivos.
Para poder aplicar este método la reacción tiene que transcurrir muy poco (sólo hasta un máximo del 10 %).
| 1,664·10⁻² | = 4 = | [A₃] | = 2 | = 4 |
| 4,16·10⁻³ | [A₂] | |||
| = 2 | ||||
Se trata de una reacción de segundo orden con relación al reactivo A.
| v₂ | = | k·[A₂]²·[B₂] | = | 4,16·10⁻³ | = 8 |
| v₁ | k·[A₁]²·[B₁] | 5,2·10⁻⁴ | |||
| 8 | = 2²·2 | = | = 1 | ||
La reacción es de orden uno con respecto al reactivo B.
La reacción global es de orden 3.
Hallamos k mediante sustitución (lo hacemos en los 3 casos y hallamos la media).
k = 3,15·10⁸ m²/s
Problema nº 2
En una reacción de primer orden se transforma el 20 % en 30 minutos. Calcular el tiempo necesario para que la transformación sea del 95 %.
| ln | C₀ | = k·t |
| C |
| ln | C₀ | = 30·k |
| 0,8·C₀ |
| k = | 1 | ·ln | 1 |
| 30 | 0,8 |
k = 7,4·10⁻³ min⁻¹
| ln | C₀ | = k·T |
| 0,05·C₀ |
| T = | 1 | ·ln | 1 |
| 7,4·10⁻³ | 0,05 |
T = 402 min
Problema nº 3
El amoníaco se descompone por acción de un filamento de tungsteno caliente según la reacción dada. La reacción se sigue por el cambio de presión, habiéndose observado a distintos tiempos los aumentos de presión reflejados en el cuadro. Sabiendo que la presión inicial era 200 torr. Calcúlese la constante de velocidad en unidades de presión.
2·NH₃ ⟶ N₂ + 3·H₂
| t(s) | 100 | 200 | 400 | 600 | 800 | 1.000 |
| p pT | 11 211 | 22,1 222,1 | 44 244 | 66,3 266,3 | 87,9 287,9 | 110 310 |
Respuesta:
Empezamos con reacciones de orden 0.
P₀ = 200 torr
| - | dC | = k·C = k ⟶ dC = k·dt |
| dt |
C₀ - C = k·t ⟶ C = C₀ - k·t
Vamos a hacer una transformación. Esta ecuación es para concentración en moles por litro, nosotros queremos trabajar con unidades de presión, por ello usaremos una expresión equivalente para la presión.
P = P₀ - k·t
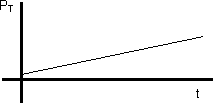
Esta gráfica no nos da ninguna información ya que necesito una representación de la P(NH₃) en función del tiempo.
P₀(NH₃) = 200 torr.
Transcurrido cierto tiempo podemos suponer que la presión disminuye.
| 2·NH₃(g) P(t) | ⟶ P₀ - x | N₂(g) x/2 | + 3·H₂(g) 3·x/2 |
pT = (P₀ - x) + x/2 + 3·x/2 = P₀ + x
Nosotros sabemos que:
pT - P₀ = x
p(NH₃) = p₀ - x = p₀ - p
| t(s) | 100 | 200 | 400 | 600 | 800 | 1.000 |
| P NH₃ | 189 | 177,9 | 156 | 133,7 | 112,1 | 90 |
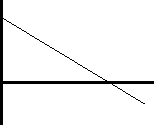
Ahora represento
p(NH₃) frente a t:
k = pendiente = 0,11
Ecuación de orden 0 ⟶ 200
Problema nº 4
La velocidad de una reacción a 30 °C es el doble que a 20 °C. Calcula la energía de activación.
Respuesta:
K = A·e⁻Ea/R·T
| v₃₀ | = 2 |
| v₂₀ |
| ln k = | -Eₐ | + ln A |
| R·T |
| ln | K₂ | = | Eₐ | ||||
| K₁ | R·( | 1 | - | 1 | ) | ||
| T₁ | T₂ | ||||||
Suponemos que los cambios de concentración son despreciables.
| v₃₀ | = | K₂ | = 2 |
| v₂₀ | K₁ |
| ln 2 = | Eₐ | ||||
| 1,987·( | 1 | - | 1 | ) | |
| 293 | 303 | ||||
| 0,693147181 = | Eₐ |
| 1,987·0,000112639 |
Eₐ = 0,693147181·1,987/0,000112639
Eₐ = 12.227 cal/mol
Eₐ = 12,22 kcal/mol
Autor: Ricardo Santiago Netto. Argentina