Como resolver un problema de química técnica paso a paso
Pasos a seguir:
1) Revisar el enunciado
2) Realizar un diagrama que nos ayude a visualizar las operaciones en bloques
3) Completar datos implícitos
4) Fijarnos en las reacciones químicas y ajustarlas
5) Seleccionar una base de cálculo
6) Analizar las ecuaciones
7) Repasar las operaciones y cuidar las unidades
8) Observar que el resultado es congruente
1)
Enunciado y datos:
| 1° | CO | 28 % |
| 2° | CO₂ | 3,5 % |
| 3° | O₂ | 0,5 % |
| 4° | N₂ | 68 % |
| 100 % | ||
Aire: O₂ 20 % en exceso.
Rendimiento: 98 %.
Gas de coque 100 gramos.
2)
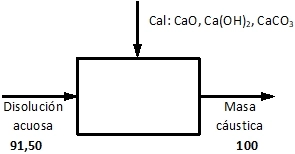
3)
El oxígeno reacciona con el monóxido de carbono ya que el dióxido no puede oxidarse más, el O₂ no reacciona consigo mismo, ni con el nitrógeno:
CO + ½·O₂ ⟶ CO₂
Base de cálculo: 100 moles de gas de coque.
| n° moles | PM | n° gramos | |
| CO | 28 | 28 | 784 |
| CO₂ | 3,5 | 44 | 154 |
| O₂ | 0,5 | 32 | 16 |
| N₂ | 68 | 28 | 1.917 |
| Total | 100 | 2.871 |
4)
Balance del O₂: moles necesarios para la combustión de todo el CO = 14 moles (tenemos ya 0,5 moles). Necesitamos 13,5 moles de O₂. El aire tiene un 20 % en exceso y la reacción es al 98 %. n° de moles de O₂ suministrado por el aire = 13,5·1,20 = 16,2 moles.
n° de moles consumidos en la combustión: 0,98·28·0,5 = 13,7 moles.
Balance del C:
C en gas de coque 28 + 3,5 = 31,5 at-gr.
C en CO en productos 28·0,02 = 0,56 at-gr.
C en CO₂ en productos 31,5 - 0,56 = 30,94 at-gr.
Balance del N₂:
N₂ en gas coque 68,0 moles
N₂ en el aire 16,2·(79/21) + 68,0 = 128,9 moles
Moles que salen:
| CO | 0,56 moles | 15,7 gramos | 0,34 % |
| CO₂ | 30,94 moles | 1.359 gramos | 18,92 % |
| O₂ | 16,2 + 0,5 - 13,7 = 3 | 96 gramos | 1,84 % |
| N₂ | 128,9 moles | 3.637 gramos | 78,9 % |
| Total | 5.107,7 gramos | 100 % |
2.871 gramos coque — 5.107,7 gramos gas combustión
100 gramos coque — x
X = 178 gramos de gas de combustión
5)
Falta detectar un componente: H₂O (84,526 %)
Se producen dos reacciones:
CaO + H₂O ⟶ Ca(OH)₂
Na₂CO₃ + Ca(OH)₂ ⟶ 2·NaOH + CaCO₃
Si aparece Na₂CO₃ es porque no es completa la reacción al igual que el Ca(OH)₂
| % | moles | PM | At-g Ca | At-g Na | At-g C | |
| CaCO₃ | 13,48 | 0,1347 | 100,1 | 0,1347 | 0,1347 | |
| Ca(OH)₂ | 0,28 | 0,00377 | 74,1 | 0,00377 | ||
| Na₂CO₃ | 0,61 | 0,00575 | 106,0 | 0,0115 | 0,00575 | |
| NaOH | 10,36 | 0,2590 | 40,0 | 0,2590 | ||
| H₂O | 75,27 | 18,0 | ||||
| Total | 100,00 | 0,1385 | 0,2705 | 0,1405 |
Base de cálculo: 100 gramos de salida.
Cogemos 1 gramo de disolución acuosa:
| Gramos | PM | moles | At-g Na | At-g C | |
| NaOH | 0,00594 | 40 | 1,49·10⁻⁴ | 1,49·10⁻⁴ | |
| Na₂CO₃ | 0,1488 | 106 | 1,40·10⁻³ | 2,80·10⁻³ | 1,40·10⁻³ |
El elemento que sirve de unión entre la disolución y lo que obtenemos es el sodio, porque nos da más información ya que entra sólo por la vía de la disolución acuosa.
Balance del Na:
Masa cáustica: 0,2705 at-gr.
En 1 g de la disolución acuosa: 0,002957 at-gr.
Masa de la disolución acuosa:
| 1 g x | — 0,002957 — 0,2705 |
X = 91,50 g de dis. ac. b
La masa de cal que hemos metido: 100 - 91,50 = 8,50 g a
Vamos a estudiar el grado de impureza de la cal:
Balance del carbono:
En la masa cáustica: 0,1405 at-gr.
En la disolución acuosa: 0,001404·91,50 g = 0,1285 at-gr.
En la cal: 0,1405 - 0,1285 = 0,0120 at-gr.
Gramos de CaCO₃ en la cal: 100·1·0,0120 = 1,20 gramos
Composición de la cal:
Masa de CaO + Ca(OH)₂ = 8,50-1,20 = 7,30 gramos
Ca en el CaCO₃ = C en el CaCO₃ = 0,0120 at-gr.
Ca en la masa cáustica = 0,1385 at-gr
Ca en forma de cal viva + apagada: 0,1385 - 0,0120 = 0,1265 at-gr.
Suponiendo que toda la cal es viva: 0,1265·56,1 = 71,0 gramos
Esto no es verdad porque nos salen 7,3 gramos. Esto quiere decir que parte está en forma de cal apagada.
| 1 mol CaO 1 mol H₂O 74,01 g Ca(OH)₂ Z | — 74,01 gramos — 18 gramos — 18 g H₂O — 0,2 g H₂O |
Ca(OH)₂ en la cal = 0,20·(74,1/18) = 0,82 gramos
7,30 - 0,82 = 6,48 g CaO
CaCO₃ = 14,1 %; Ca(OH)₂ = 9,6 %; CaO = 76,3 %;
CaO activo total = 0,1265 moles de Ca(OH)₂
Na₂CO₃ en disolución 0,001404 moles de Na₂CO₃ (1gr)·91,5 = 0,1285 moles de Na₂CO₃
El reactivo limitante es la cal apagada. Exceso de Na₂CO₃ = 0,1285 - 0,1265 = 0,0020 moles.
| % en exceso = | 0,0020 | ·100 |
| 0,1265 |
% en exceso = 1,6 % de Na₂CO₃
El grado de conversión se hace sobre el reactivo limitante: La cal.
1° tabla: Ca(OH)₂ 0,00377 moles de cal apagada sin reaccionar. n° moles de CaO = 0,1265
| 100 - | 0,00377 | ·100 = 97 % |
| 0,1265 |
6)
El reactivo limitante no existe en los productos.
| % | kg | PM | kmol | Na(Kat) | S(Kat) | Cl(Kat) | |
| Na₂SO₄ | 91,48 | 0,9148 | 142,1 | 0,00644 | 0,01288 | 0,00644 | |
| NaHSO₄ | 4,79 | 0,0479 | 120,1 | 0,000398 | 0,000398 | 0,000398 | |
| NaCl | 1,98 | 0,0198 | 58,5 | 0,000338 | 0,000338 | 0,000338 | |
| H₂O | 1,35 | 0,0135 | 18 | ||||
| HCl | 0,40 | 0,0040 | 36,5 | 0,000110 | 0,000110 | ||
| 100 | 1 | 0,01362 | 0,00684 | 0,000448 |
Base de cálculo: 1.000 kg de NaCl
Torta de sal: 1 kg.
Dis. H₂SO₄: 1 kg.
| 0,01288 | ·100 = 94,5 % |
| 0,01362 |
Todo el sodio del Na₂SO₄ partido del total.
| Moles de NaCl = | 1.000 |
| 58,5 |
Moles de NaCl = 17,08 kmol de NaCl = 17,08 Kat Na.
| 1 kg "torta" x | — 0,01362 Kat Na. — 17,08 Kat Na |
x = 1.253 kg
En el caso del ácido el nexo es el azufre:
| 0,75 | = 0,00764 kmol de H₂SO₄ puro |
| 98 |
Kat de S: 0,00684·1.253 = 8,58 Kat en la torta.
Pero de la disolución ácida:
| 8,58 | = 1.123 kg |
| 0,00764 |
| 1 kg ácido y | — 0,00764 Kat de S — 8,58 Kat de S |
El agua se incorpora en una disolución al 75 % de H₂O.
Balance del H₂O:
| 1.123 kg disolución×0,25 100-0,75 % | = | Vapor + torta de sal 0,0135·1.253 = 17 kg |
7)
CH₂ = CH₂ + ½·O₂ ⟶ CH₂OCH₂
CH₂ = CH₂ + 3·O₂ ⟶ 2·CO₂ + H₂O
CH₂ = CH₂ + O₂ ⟶
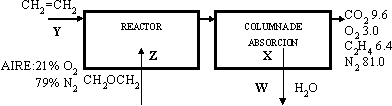
Base de cálculo: 100 kmol de gas residual.
Balance del N₂: 0,79·Z = 81,0 ⟶ Z = 102,5 kmol
Balance del O₂: 0,21·Z = ½·X + ½·W + 3,0 + 9,6
Balance del C: 2·Y = 2·X + 9,6 + 2·6,4
Balance del H₂: 2·Y = 2·X + W + (2·6,4)
X = 8,25 kmol CH₂OCH₂
Y = 19,45 kmol CH₂ = CH₂
W = 9,6 kmol H₂O
| X | ·100 = 42,4 % CH₂ |
| Y |
CH₂: reacciona.
| 6,4 | ·100 = 32,9 % CH₂ |
| 19,5 |
CH₂ no reacciona.
Autor: Javier Zuluaga.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).