Problema nº 2 de electrólisis. Leyes de Faraday, masa y volumen depositados en un electrodo - TP01

Enunciado del ejercicio nº 2

En una cuba electrolítica que contiene cloruro cúprico fundido se hace pasar una cierta cantidad de corriente durante 3 horas, observando que se deposita cobre metálico en el cátodo y se desprende cloro gaseoso en el ánodo.

a) Determinar la cantidad de corriente necesaria para depositar 20 g de cobre.

b) Calcular el volumen de cloro obtenido a 25 °C y 1 atm.

Desarrollo

Datos:

t = 3 h

m _Cu = 20 g

t° = 25 °C

p = 1 atm.

ζ_Cu = 0,000329 g/C *

ζ_Cl = 0,000367 g/C *

* Dato de tabla

Fórmulas:

m = ζ·i·t

Solución

a)

Adecuamos las unidades:

t = 3 h = 3 h·3.600 s/h

t = 10.800 s

Aplicamos la primera ley de Faraday:

m = ζ_Cu·i·t

Despejamos i:

Reemplazamos por los datos y calculamos:

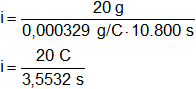
Recordemos que C/s = A.

i = 5,628729033 A

Respuesta a): la corriente requerida es de 5,63 A

b)

Calculamos masa de cloro Cl₂ obtenida con la corriente calculada en el punto anterior.

m_Cl = ζ_Cl·i·t

Reemplazamos por los datos y calculamos:

m_Cl = 0,000367 g/C·5,628729033 A·10.800 s

m_Cl = 22,3100304 g

Este valor es en CNPT, por lo tanto, hallamos los moles de cloro Cl₂:

1 Mol _Cl = 2·35,453 g = 70,906 g

n = 0,314642349 moles de cloro.

Para hallar el volumen debemos emplear la ecuación de estado de los gases.

p·V = n·R·T

Donde:

R es la constante de los gases.

T se mide en grados kelvin.

Adecuamos las unidades:

T = 25 °C + 273 °C

T = 298 K

Despejamos V:

Reemplazamos por los datos y calculamos:

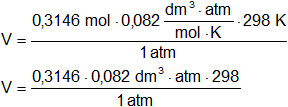
V = 7,688600439 dm³

Respuesta b): el volumen de cloro obtenido es 7,689 dm³.

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP01
• | Siguiente ›

Ejemplo, cómo calcular la masa y el volumen que se depositan en un electrodo