Problema nº 4 de electrólisis. Fórmula-gramo dada la constante de equilibrio - TP03

Enunciado del ejercicio nº 4

Calcular cuantas fórmula-gramo oxhidrilo se hallan disociadas en 1 litro de solución 0,1 M de NH₄OH.

Desarrollo

El NH₄OH desprende un ion oxhidrilo o hidroxilo (valencia = 1), por lo tanto, 0,1 M = 0,1 N.

Datos:

V = 1 l

C = 0,1 M

k_b = 1,8·10⁻⁵ (Constante de disociación del NH₄OH a 25 °C)

Solución

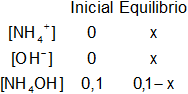
Aplicamos la constante de equilibrio para una base (k_b):

Reemplazamos:

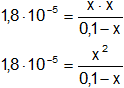
1,8·10⁻⁵·(0,1 - x) = x²

Igualamos a cero:

x² - 1,8·10⁻⁵·(0,1 - x) = 0

Aplicamos distributiva del producto con respecto a la resta:

x² - 1,8·10⁻⁶ + 1,8·10⁻⁵·x = 0

x² + 1,8·10⁻⁵·x - 1,8·10⁻⁶ = 0

Aplicamos la ecuación de Báscara o Bhaskara:

Siendo:

a = 1

b = 1,8·10⁻⁵

c = -1,8·10⁻⁶

Reemplazamos y resolvemos, obtendremos dos valores:

Resolvemos:

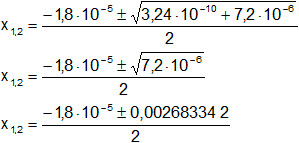
Calculamos los valores por separado según el signo del resultado de la raíz:

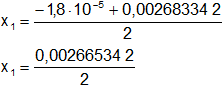
x₁ = 0,001332671 mol/l

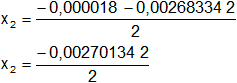
x₂ = -0,001350671 (descartamos por < 0)

La fórmula-gramo o peso fórmula-gramo es el peso molecular o mol de una sustancia, como vemos el resultado está expresado en moles por litro, o sea, fórmula-gramo por litro.

Respuesta: en 1 litro de solución 0,1 M de NH₄OH hay 1,33·10⁻³ fórmula-gramo oxhidrilo.

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo, cómo calcular la fórmula-gramo dada la constante de equilibrio