Problema nº 4 de electrólisis. Porcentaje de ionización y ka - TP05

Enunciado del ejercicio nº 4

Calcular el porcentaje de ionización del ácido acético en una solución 0,1 M. Consulte el valor de kₐ en la tabla de constantes de ionización.

Expresamos la ecuación balanceada de disociación:

CH₃COOH + H₂O ⇌ H₃O⁺ + CH₃COO⁻

Planteamos los moles iniciales y en el equilibrio:

La constante de equilibrio para un ácido (kₐ) es:

kₐ =	[H₃O⁺]·[CH₃COO⁻]
	[CH₃COOH]

Reemplazamos por los datos:

1,80·10⁻⁵ =	x·x
	0,1 - x

1,80·10⁻⁵ =	x²
	0,1 - x

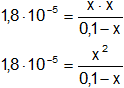
1,80·10⁻⁵·(0,1 - x) = x²

Igualamos a cero:

x² - 1,80·10⁻⁵·(0,1 - x) = 0

Aplicamos distributiva del producto con respecto a la resta:

x² + 1,80·10⁻⁵·x - 1,80·10⁻⁶ = 0

Aplicamos la ecuación de Báscara o Bhaskara:

x_1,2 =	-b ± √b² - 4·a·c
	2·a

Siendo:

a = 1

b = 1,80·10⁻⁵

c = -1,80·10⁻⁶

Reemplazamos y resolvemos, obtendremos dos valores:

x_1,2 =	-0,000018 ± √0,000018² - 4·1·(-0,0000018)
	2·1

x_1,2 =	-0,000018 ± √0,0000072003240
	2

x_1,2 =	-0,000018 ± 0,002683342
	2

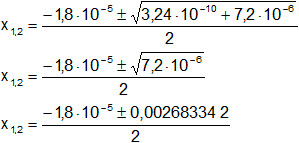
Calculamos los valores de x_1,2 por separado según el signo del resultado de la raíz:

x₁ =	-0,000018 + 0,002683342
	2

x₁ =	0,0026653
	2

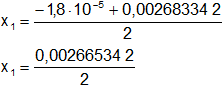
x₁ = 1,33·10⁻³ mol/l

x₂ =	-0,000018 - 0,002683342
	2

x₂ =	-0,0027013
	2

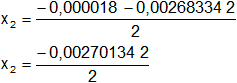
x₂ = -1,35·10⁻³ mol/l (se descarta por < 0)

[CH₃COOH] = 0,1 M

[H₃O⁺] = [CH₃COO⁻]

x₁ = [H₃O⁺] = 1,33·10⁻³ mol/l

El porcentaje de ionización es:

Porcentaje de ionización =	[H₃O⁺]·100
	[CH₃COOH]

Reemplazamos por los datos y calculamos:

Porcentaje de ionización =	1,33·10⁻³·100
	0,1

Porcentaje de ionización =	1,33·10⁻¹·1
	0,1

Porcentaje de ionización = 1,33 %

Respuesta: el porcentaje de ionización del ion CH₃COO⁻ es 1,33 %.

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular el porcentaje de ionización