Problema nº 9 de electrólisis. Primera ley de Faraday, masa depositada en un electrodo y tiempo que demora - TP06

Enunciado del ejercicio nº 9

En una cuba electrolítica se tiene en el cátodo una pieza cúbica de bronce de 3 cm de lado que se desea cromar con 0,03 mm de espesor. Para ello se emplea una disolución de cloruro de cromo III (CrCl₃), δ = 7,19 g/cm³. Se hace circular una corriente de 20 A. ¿Qué masa de cromo se empleará? ¿Cuánto tiempo demorará el proceso?

Desarrollo

Datos:

l = 3 cm

d = 0,03 mm

i = 20 A

δ_Cr = 7,19 g/cm³

ζ_Cr³⁺ = 0,000180 g/C (Dato de tabla)

Fórmulas:

m = ζ·i·t

Solución

a)

Para calcular la masa de cromo del recubrimiento, primero debemos hallar el volumen total de dicho recubrimiento. Para ello calculamos la superficie total del cubo y luego, conocido el espesor deseado, calculamos el volumen.

V = S·d

V = l²·d

Adecuamos las unidades:

d = 0,03 mm = 0,03 mm·(1 cm/10 mm)

d = 0,003 cm

Reemplazamos por los datos y calculamos:

V = (3 cm)²·0,003 cm

V = 9 cm²·0,003 cm

V = 0,027 cm³

Tenemos el volumen, ahora empleamos la fórmula de densidad para hallar la masa:

Despejamos m:

m = δ_Cr·V

Reemplazamos por los valores y calculamos:

m = 7,19 g/cm³·0,027 cm³

m = 0,19413 g

Respuesta a): la masa de cromo que debe depositarse en el cubo es 0,19 g.

b)

Para calcular el tiempo aplicamos la primera ley de Faraday:

m = ζ·i·t

Despejamos t:

Reemplazamos por los valores y calculamos:

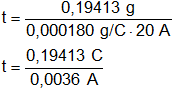
t = 53,925 s

Respuesta b): el tiempo que demanda el proceso es 54 s.

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP06
• | Siguiente ›

Ejemplo, cómo calcular la masa de un elemento que se deposita en el electrodo y tiempo que demora