Problema nº 7 de electrólisis. Primera ley de Faraday, corriente requerida - TP07

Enunciado del ejercicio nº 7

El peróxido de hidrógeno puede obtenerse por las reacciones sucesivas:

La primera reacción es una reacción electrolítica y la segunda una destilación de vapor de agua. ¿Qué corriente tendría que utilizarse en la primera reacción de modo que se obtenga suficiente producto intermedio para producir 100 g de peróxido de hidrógeno puro por hora? Supóngase un rendimiento del 50 %.

Desarrollo

Datos:

m = 100 g

t = 1 h

η = 0,5

ζ_H⁺ = 0,000010 g/C *

* Dato de tabla

Fórmulas:

m = ζ·i·t

Solución

La ecuación estequiométrica balanceada de la primera ecuación es la siguiente:

2·NH₄HSO₄ ⟶ H₂ + (NH₄)₂S₂O₈

Calculamos el mol de cada compuesto que interviene en la reacción:

2·NH₄HSO₄: 2·(14,0067 g + 5·1,00797 g + 32,064 g + 4·15,9994) = 230,2163 g

H₂: 2·1,00797 g = 2,01594 g

(NH₄)₂S₂O₈: 2·(14,0067 g + 4·1,00797 g) + 2·32,064 + 8·15,9994 = 228,20036 g

La ecuación estequiométrica balanceada de la segunda ecuación es la siguiente:

(NH₄)₂S₂O₈ + 2·H₂O ⟶ 2·NH₄HSO₄ + H₂O₂

Calculamos el mol de cada compuesto que interviene en la reacción:

(NH₄)₂S₂O₈: 2·(14,0067 g + 4·1,00797 g) + 2·32,064 + 8·15,9994 = 228,20036 g

2·H₂O: 2·(2·1,00797 g + 15,9994 g) = 36,03068 g

2·NH₄HSO₄: 2·(14,0067 g + 5·1,00797 g + 32,064 g + 4·15,9994) = 230,2163 g

H₂O₂: 2·1,00797 g + 2·15,9994 g) = 34,01474 g

Con las ecuaciones balanceadas y con los datos de las masas que intervienen de cada sustancia, planteamos:

Para obtener 34,01474 g de H₂O₂ se necesitan 228,20036 g de producto intermedio [(NH₄)₂S₂O₈] o, lo que es equivalente, 2,01594 g de H₂ que se desprenderán en el cátodo.

Realizamos los cálculos para 100 g de H₂O₂:

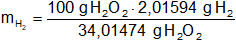
m_H₂ = 5,92666591 g de H₂

Dado que el rendimiento del proceso es del 50 %, realizamos la corrección:

m_H₂f = m_H₂÷η

m_H₂f = 5,92666591 g de H₂÷0,5

m_H₂f = 11,85333182 g

Con estos datos aplicamos la primera ley de Faraday para el hidrógeno:

m = ζ·i·t

Despejamos i:

Adecuamos las unidades:

t = 3.600 s

Reemplazamos por los valores dados y resolvemos:

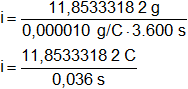
i = 329,2592172 A

Respuesta, la corriente requerida en la primera reacción es:

i = 329 A

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP07
• | Siguiente ›

Ejemplo, cómo calcular la corriente necesaria para que un elemento se deposite en el electrodo