Problema nº 5 de equilibrio químico, los gases, el porcentaje de disociación y el grado de disociación - TP03
Enunciado del ejercicio nº 5
A 27 °C de temperatura y a 1 atm. de presión, el N₂O₄ está disociado en un 20 % en NO₂. Calcular:
a) El valor de kₚ.
b) El porcentaje de disociación a 27 °C y con una presión total de 0,1 atm.
c) ¿Cuál es el grado de disociación de una muestra de 69 g de N₂O₄ dentro de un recipiente de 20 litros a 27 °C?
Solución
Expresamos la ecuación equilibrada de la reacción:
a)
Para esta reacción tomamos un mol de N₂O₄, ya que no especifica la cantidad.
Porcentaje de disociación: 20 % ≡ 0,2
Planteamos los moles iniciales y en el equilibrio, y el gas total:
| Inicial | Equilibrio | Gas total | Fracción molar | Presión parcial | |
|---|---|---|---|---|---|
| N₂O₄ | 1 | 1 - 0,2 = 0,8 | 1 | 0,8÷1,2 = 0,6667 | 0,67 |
| NO₂ | 0 | 0,2·2 = 0,4 | 1,2 | 0,4÷1,2 = 0,3333 | 0,33 |
Verificamos que la suma de las fracciones molares sea igual a 1:
0,6667 + 0,3333 = 1
La suma de las presiones parciales también es igual a 1 atm, se corresponde con el enunciado.
Aplicamos la fórmula de la constante de equilibrio de presiones parciales:
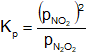
Reemplazamos por los datos y calculamos:
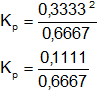
Kₚ = 0,1667
Respuesta a): la constante de equilibrio de presiones parciales Kₚ = 0,17 atm.
b)
El grado de disociacón es:
Planteamos los moles iniciales y en el equilibrio, y el gas total para 0,1 atm:
| Inicial | Equilibrio | Gas total | Fracción molar | Presión parcial | |
|---|---|---|---|---|---|
| N₂O₄ | 1 | 1 - α | 1 | (1 - α)÷(1 + α) | (1 - α)÷(1 + α)·0,1 |
| NO₂ | 0 | 2·α | 1 + α | 2·α÷(1 + α) | 2·α÷(1 + α)·0,1 |
Aplicamos la fórmula de la constante de equilibrio de presiones parciales:
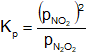
Reemplazamos por los datos y calculamos:
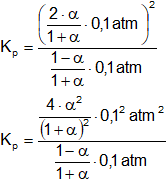
Simplificamos:
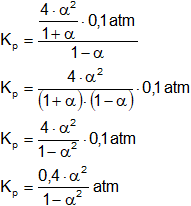
Siendo Kₚ = 0,17 atm
0,17·(1 - α²) = 0,4·α²
Aplicamos distributiva del producto con respecto a la resta:
0,17 - 0,17·α² = 0,4·α²
Despejamos α:
0,4·α² + 0,17·α² = 0,17
0,57·α² = 0,17
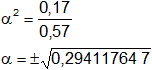
α = ±0,542326145
Se toma el valor positivo de α.
α = 0,542326145 ≡ 54 %
Verificamos que cumpla con el principio de Le Châtelier:
En la reacción intervienen más volúmenes de productos que de reactantes. Cumplea con el principio de Le Châtelier, la reacción se desplaza a la derecha.
Respuesta b): el grado de disociación de la muestra es 54 %.
c)
El grado de disociacón es:
Un mol de N₂O₄ = 92,011 g
Pide el grado de disociación de una muestra de 69 g de N₂O₄.
Planteamos los moles iniciales y en el equilibrio, y el gas total:
| Inicial | Equilibrio | Gas total | Fracción molar | Presión parcial | |
|---|---|---|---|---|---|
| N₂O₄ | 0,75 | 0,75·(1 - α) | 0,75 | (1 - α)÷(1 + α) | (1 - α)÷(1 + α)·P |
| NO₂ | 0 | 2·0,75·α | P | 2·α÷(1 + α) | 2·α÷(1 + α)·P |
Hallamos la presón total. Aplicamos la ecuación de estado de los gases:
p·V = n·R·T
Despejamos la presión P:
Adecuamos la temperatura:
T = 27 °C +273 °C = 300 K
Reemplazamos por los datos:
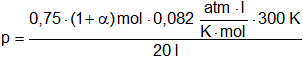
Simplificamos:
Resolvemos:
P = 0,9225·(1 + α) atm (1)
Aplicamos la fórmula de la constante de equilibrio de presiones parciales:
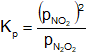
Reemplazamos por los datos y calculamos:
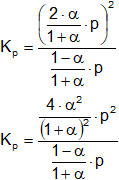
Simplificamos:
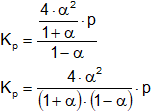
Reemplazamos P de la (1):
Simplificamos:
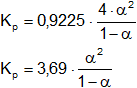
Tomamos Kₚ = 0,1667
0,1667·(1 - α) = 3,69·α²
Aplicamos distributiva del producto con respecto a la resta:
0,1667 - 0,1667·α = 3,69·α²
Igualamos a cero:
3,69·α² + 0,1667·α - 0,1667 = 0
Aplicamos la ecuación de Báscara o Bhaskara:
Siendo:
a = 3,69
b = 0,1667
c = -0,1667
Reemplazamos y resolvemos, obtendremos dos valores:
Calculamos los valores de α1,2 por separado según el signo del resultado de la raíz:
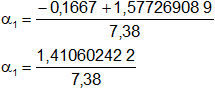
α₁ = 0,19113854
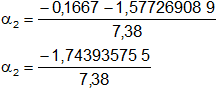
α₂ = -0,236305658 (se descarta por ser negativo)
α = 0,19113854
Respuesta c): el grado de disociación de la muestra de 69 g de N₂O₄ es 19,11 %.
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo, cómo calcular la constante de equilibrio de los gases, el porcentaje de disociación y el grado de disociación