Problema nº 3 de equilibrio químico, las presiones parciales y los moles - TP04

Enunciado del ejercicio nº 3

Se calientan un mol de yodo y un mol de hidrógeno en un recipiente de 30 litros a 448 °C, siendo K = 50 para esta temperatura. Se pide:

a) ¿Cuántos moles de yodo quedan sin reaccionar al alcanzar el equilibrio?

b) ¿Cuál es la presión total en el recipiente?

c) ¿Cuál es la presión parcial del yodo y del yoduro de hidrógeno en la mezcla en el equilibrio?

d) Luego se agrega un mol de hidrógeno al sistema en el equilibrio. ¿Cuántos moles de yodo original quedarán sin reaccionar?

Desarrollo

Datos:

K = 50

t° = 448 °C

Moles _I = 1

Moles _H = 1

Moles _HI = x

V = 30 l

Solución

Como el volumen del recipiente es de 1 l, las concentraciones en todos los casos quedan indicados por los valores absolutos de moles de cada sustancia.

Expresamos la ecuación equilibrada de la reacción:

H₂ + I₂ ⇌ 2·HI

a)

x será el número de moles de yodo y de hidrógeno en el equilibrio.

En el equilibrio desaparecen x moles de hidrógeno y x moles de yodo para formar 2·x moles de yoduro de hidrógeno.

[H₂] = (1 - x) mol/l

[I₂] = (1 - x) mol/l

[HI] = 2·x mol/l

Aplicamos la fórmula de la constante de equilibrio:

K·(1 - x)² = 4·x²

K·(1 - 2·x + x²) = 4·x²

K - 2·K·x + K·x² = 4·x²

K - 2·K·x + K·x² - 4·x² = 0

Reemplazamos por los datos y calculamos:

50 - 2·50·x + 50·x² - 4·x² = 0

50 - 100·x + 46·x² = 0

46·x² - 100·x + 50 = 0

Aplicamos la ecuación general:

Donde:

a = 46

b = -100

c = 50

Reemplazamos y resolvemos, obtendremos dos valores:

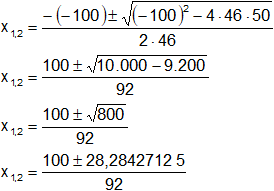
Calculamos por separado x₁ y x₂ según el signo:

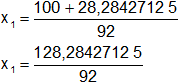
x₁ = 1,394394253 > 1, se descarta porque la reacción es incompleta.

x₂ = 0,779518791

Luego:

[H₂] = (1 - x) mol/l

[H₂] = (1 - 0,779518791) mol/l

[H₂] = 0,220481209 mol/l

[I₂] = (1 - x) mol/l

[I₂] = (1 - 0,779518791) mol/l

[I₂] = 0,220481209 mol/l

[HI] = 2·x mol/l

[HI] = 2·0,779518791 mol/l

[HI] = 1,559037582 mol/l

Respuesta a), los moles de yodo que quedan sin reaccionar son:

[I₂] = 0,22 mol/l

b)

Antes, durante y luego de la reacción, el número total de moles permanece constante aunque la reacción no sea completa:

El número total de moles es 2 (n = 2)

Aplicamos la ecuación de estado de los gases:

p·V = n·R·T

Despejamos la presión P:

Adecuamos la temperatura:

T = 448 °C + 273 °C = 721 K

Reemplazamos por los datos:

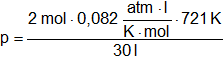
Resolvemos:

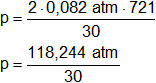
P = 3,941466667 atm

Respuesta b), la presión total en el recipiente es:

P = 3,94 atm

c)

Aplicamos la fórmula de presión parcial:

Reemplazamos por los datos y calculamos:

p_H2 = 0,434509668 atm

Reemplazamos por los datos y calculamos:

p_I2 = 0,434509668 atm

p_HI = P - (p_H2 + p_I2)

Reemplazamos por los datos y calculamos:

p_HI = 3,941466667 atm - (0,434509668 atm + 0,434509668 atm)

p_HI = 3,941466667 atm - 0,869019337 atm

p_HI = 3,07244733 atm

Resultado d), la presión parcial del yodo y del yoduro de hidrógeno en la mezcla en el equilibrio es:

p_I2 = 0,43 atm

p_HI = 3,07 atm

d)

Repetimos el ítem (a) agregando 1 mol de hidrógeno.

x será el número de moles de yodo y de hidrógeno en el equilibrio.

En el equilibrio desaparecen x moles de hidrógeno y x moles de yodo para formar 2·x moles de yoduro de hidrógeno.

[H₂] = (2 - x) mol/l

[I₂] = (1 - x) mol/l

[HI] = 2·x mol/l

Aplicamos la fórmula de la constante de equilibrio:

K·(2 - x)·(1 - x) = 4·x²

K·(2 - 2·x - x + x²) = 4·x²

K·(2 - 3·x + x²) = 4·x²

2·K - 3·K·x + K·x² = 4·x²

2·K - 3·K·x + K·x² - 4·x² = 0

Reemplazamos por los datos y calculamos:

2·50 - 3·50·x + 50·x² - 4·x² = 0

100 - 150·x + 46·x² = 0

46·x² - 150·x + 100 = 0

Aplicamos la ecuación general:

Donde:

a = 46

b = -150

c = 100

Reemplazamos y resolvemos, obtendremos dos valores:

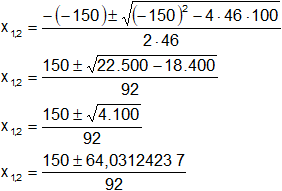
Calculamos los valores de x_1,2 por separado según el signo del resultado de la raíz:

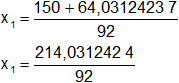
x₁ = 2,326426548 (se descarta porque solo hay 1 mol del reactivo limitante)

x₂ = 0,934443018

Luego:

[H₂] = (2 - x) mol/l

[H₂] = (2 - 0,934443018) mol/l

[H₂] = 1,065556982 mol/l

[I₂] = (1 - x) mol/l

[I₂] = (1 - 0,934443018) mol/l

[I₂] = 0,065556982 mol/l

[HI] = 2·x mol/l

[HI] = 2·0,934443018 mol/l

[HI] = 1,868886035 mol/l (aún incompleta)

Respuesta d), los moles de yodo que quedan sin reaccionar son:

[I₂] = 0,066 mol/l

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo, cómo calcular los moles y las presiones parciales de una mezcla de gases en el equilibrio