Ecuación de estado de los gases ideales
Definimos como gas ideal o perfecto al gas que cumple exactamente con las leyes de Boyle y Mariotte y de Charles y Gay Lussac.
La ecuación de estado de los gases describe el estado de agregación de la materia como una relación matemática, se expresa de la siguiente forma:
p·V = n·R·T
Donde R es la constante universal de los gases, su valor es:
![]()
Desarrollo de la ecuación
Partiendo de la ecuación general de los gases y conociendo la temperatura, la presión y el volumen que ocupa una determinada masa de gas se puede calcular qué valor tendrá una de esas tres magnitudes cuando varían las otras dos. Y obtendremos lo mismo con cada variación, un valor constante (k):
![]()
Calculamos el valor de k para un mol de gas en CNPT, es decir:
p = 1 atmósfera
T = 0 °C = 273 K
V = 22,4 dm³ (volumen molar)
![]()
Calculamos:
![]()
A k se la conoce como R, definida anteriormente, para 1 mol.
![]()
Los valores de cálculo son para un mol de cualquier gas ideal dado que empleamos el volumen molar.
Luego la ecuación (1) queda:
![]()
p·V = R·T (2)
Las unidades empleadas son de uso corriente en Química, lo correcto es expresar las unidades según el sistema internacional de unidades.
p = 101325 Pa (Pascal)
T = 273 K
V = 0,0224 m³ (volumen molar)
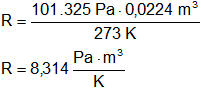
En este apunte continuaremos con las unidades usuales de Química.
La ecuación (2) corresponde al cálculo para un mol de gas, si realizamos el cálculo para un valor n distinto a un mol tendremos:
p·V = n·R·T (3)
Donde n es el número de moles que intervienen.
Otras expresiones de la ecuación
En función de la masa
Podemos expresar la misma ecuación para el caso de la masa de un gas sabiendo que:
m = n·mol
![]()
Donde m es la masa de gas que interviene expresada en gramos (g).
Reemplazando en la ecuación (3):
![]() (4)
(4)
Ejemplo:
¿Cuántos gramos hay en 10 m³ de oxígeno a 4 atmósferas y 27 °C?
![]()
Datos:
V = 10 m³ = 10.000 dm³
p = 4 atmósferas
T = 27 °C = 300 K
Mol = 32 g
Despejamos m:
![]()
Reemplazamos por los datos y calculamos:
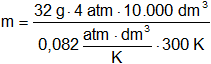
m = 52.032,52 g
Resultado:
m = 52,032 kg
En función de la densidad
A partir de la ecuación (4), que sigue siendo la ecuación de estado de los gases, podemos expresarla con la variable densidad (δ). Sabiendo que:
![]()
Donde δ es densidad del gas que interviene expresada en gramos (g/dm³).
![]()
Despejamos p:
![]()
Reemplazamos:
![]()
Ejemplo:
Siendo el mol de oxígeno 32 g y el volumen molar 22,4 dm³. ¿Cuál es la densidad del oxígeno?
Datos:
V = 22,4 dm³
p = 1 atmósfera
T = 273 K
Mol = 32 g
Suponemos CNPT, despejamos δ:
![]()
![]()
Reemplazamos por los datos y calculamos:
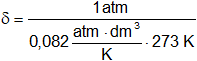
Resultado:
δ = 1,4295 g/dm³
Conceptos
Un gas ideal es un gas imaginario cuyas partículas no tienen diámetro ni se atraen mutuamente.
El volumen de un gas no solo depende del número de partículas sino también de la temperatura y de la presión.
Bibliografía:
Héctor Fernández Serventi. "Química general e inorgánica". Losada S. A., Buenos Aires.
Robert C. Smoot y Jack Price. "Química, Un curso moderno". Compañía Editorial Continental S. A., México.
Autor: Ricardo Santiago Netto. Argentina
¿Cuál es la ecuación de estado de los gases ideales?