Problema nº 5 de gases ideales, variación de la densidad de un gas - TP02

Enunciado del ejercicio nº 5

Sabiendo que el peso atómico del cloro es de 35,5; calcular su densidad en CNPT y luego a 200 °C y 5 atmósferas.

Masa atómico = 35,5 g

V₁ = 22,4 dm³

p₁ = 1 atm

p₂ = 5 atm

T₁ = 273 K

T₂ = 200 °C = 473 K

Calculamos la masa de un mol de cloro:

Mol de Cl₂: 2·35,5 g = 71 g

Calculamos la densidad de un mol en CNPT:

Reemplazamos por los datos y calculamos:

Resultado, la densidad del cloro en CNPT es:

δ₁ = 3,15 g/dm³

En el segundo caso la masa se mantiene constante, lo que varía es el volumen.

De la ecuación general de los gases ideales despejamos V₂:

Reemplazamos por los datos y calculamos:

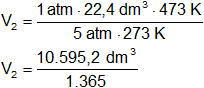
Cálculo de volumen

V₂ = 7,7621 dm³

Con este dato y la masa calculamos la densidad a 200 °C y 5 atmósferas:

Reemplazamos por los datos y calculamos:

Resultado, la densidad del cloro a 200 °C y 5 atmósferas es:

δ₂ = 9,15 g/dm³

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo de cómo determinar la variación de la densidad de un gas