Problema n° 9 de gases ideales, volumen y densidad de un gas - TP04

Enunciado del ejercicio n° 9

Se obtienen 55 cm³ de nitrógeno a 22 °C y presión atmosférica de 755 mm de Hg, determinar:

a) El volumen normal.

b) La densidad a 20 °C.

Desarrollo

Datos:

V₁ = 55 cm³

p₁ = 755 mm de Hg

p₂ = 1 atm

T₁ = 22 °C

T₂ = 0 °C

T₃ = 20 °C

R = 0,08205 atm·dm³/K·mol

Fórmulas:

p·V·PM = m·R·T

Solución

Adecuamos las unidades:

p₁ = 0,9934 atm

V₁ = 55 cm³ = 0,055 dm³

T₁ = 22 °C = 295 K

T₂ = 0 °C = 273 K

T₃ = 20 °C = 293 K

a)

Aplicamos la ecuación general de los gases ideales, despejamos V₂:

Reemplazamos por los datos y calculamos:

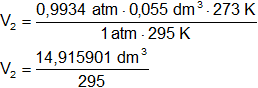
Resultado, el volumen final del gas es:

V₂ = 0,050563 dm³

b)

Calculamos la masa de un mol de nitrógeno gaseoso:

PM N₂: 2·14,0067 g = 28,0134 g

Aplicamos la ecuación estado de los gases ideales para determinar la masa de nitrógeno, despejamos "m":

Reemplazamos por los datos y calculamos:

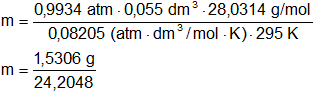
m = 0,0632 g

Aplicamos la ecuación general de los gases ideales para T₃, despejamos V₃:

Reemplazamos por los datos y calculamos:

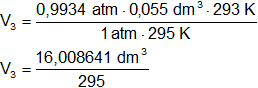
V₃ = 0,054268 dm³

Aplicamos la fórmula de densidad con los datos hallados:

Resultado, la densidad del nitrógeno a 20 °C es:

δ = 1,165 g/dm³

Autor: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo, cómo determinar la densidad de un gas