Problema nº 10 de gases ideales, masa y densidad de un gas - TP13

Enunciado del ejercicio nº 10

¿Qué masa de cinc debe disolverse en ácido sulfúrico para obtener 500 cm³ de hidrógeno a 20 °C y 770 mm Hg?

t = 20 °C

p = 770 mm Hg

R = 0,08205 atm·dm³/K·mol

V_molar = 22,4 dm³ CNPT

p·V·mol = m·R·T

La ecuación estequiométrica balanceada es la siguiente:

H₂SO₄(ac) + Zn(s) ⟶ ZnSO₄(s) + H₂(g)

Calculamos el mol de cada compuesto que interviene en la reacción:

H₂SO₄: 2·1,00797 g + 32,064 g + 4·15,9994 g = 98,07754 g

Zn: 65,37 g = 65,37 g

ZnSO₄: 65,37 g + 32,064 g + 4·15,9994 g = 161,4316 g

H₂: 2·1,00797 g = 2,01594 g

Hallamos las masas de los moles que intervienen en la reacción balanceada, la suma de las masas de ambos miembros debe ser igual:

Estos cálculos son independientes de las condiciones de temperatura y presión.

Aplicamos la ecuación de estado de los gases en función del peso molecular, despejamos "m":

p·V·mol = m·R·T

Convertimos las unidades de temperatura:

T = 20 °C + 273 °C

T = 293 K

Convertimos las unidades de presión:

p = 1,013157895 atm

Convertimos las unidades de volumen:

V_H₂ = 0,5 dm³

Reemplazamos por los datos y calculamos:

Cálculo de la masa de un gas

m_H₂ = 0,042479416 g de H₂

Luego hallamos la masa de cinc necesaria para obtener 0,5 dm³ (500 cm³) de hidrógeno:

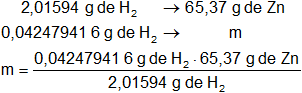
Cálculo de la masa en una reacción química

m_Zn = 1,377461333 g de Zn

Resultado: la masa de cinc que debe disolverse en ácido sulfúrico para obtener 500 cm³ de hidrógeno a 20 °C y 770 mm Hg es 1,38 g.

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo de cómo determinar la masa de un gas en una reacción