Problema nº 5 cálculo de densidad de la materia. Densidad de un objeto - TP08

Enunciado del ejercicio nº 7

Una aleación ha sido mecanizada en forma de disco plano de 3,15 cm de diámetro y 0,45 cm de espesor, con un orificio central de 0,75 cm de diámetro. El disco pesa 20,2 g. ¿Cuál es la densidad de la aleación?

Desarrollo

Datos:

D = 3,15 cm

d = 0,75 cm

e = 0,45 cm

m = 20,2 g

Fórmulas:

V = π·(½·D)²·e (volumen del cilindro)

Solución

El volumen de la pieza en forma de disco es:

V = π·(½·D)²·e - π·(½·d)²·e

Al volumen del cilindro de diámetro D se la resta el volumen del cilindro del orificio (d).

V = ¼·π·e·(D² - d²)

Reemplazamos V en la fórmula de densidad:

Reemplazamos por los datos y calculamos:

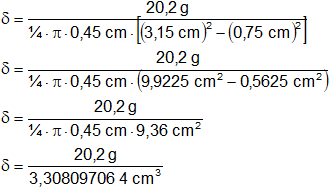
δ = 6,106229536 g/cm³

Resultado, la densidad del disco plano es:

δ = 6,1 g/cm³

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP08
• | Siguiente ›

Ejemplo de cómo determinar la densidad