Problema nº 6 de ecuaciones de óxido reducción, igualación - TP03
Enunciado del ejercicio nº 6
Balancee las siguientes ecuaciones después de representarlas en forma iónica neta:
a) Cu + HNO₃ ⟶ Cu(NO₃)₂ + NO + H₂O
b) Fe(NO₃)₂ + HNO₃ ⟶ Fe(NO₃)₃ + NO + H₂O
c) Zn + HNO₃ ⟶ Zn(NO₃)₂ + NO₂ + H₂O
d) Sb + H₂SO₄ ⟶ Sb₂(SO₄)₃ + SO₂ + H₂O
e) H₂S + H₂SO₃ ⟶ S + H₂O
Solución
a) Reacción de oxidación del cobre metálico por el ácido nítrico con formación de ion cúprico y óxido nítrico.
Cu + HNO₃ ⟶ Cu(NO₃)₂ + NO + H₂O
Primero disociamos los compuestos detallando el número de oxidación:
Cu° + H⁺ + N⁵⁺ + 3·O²⁻ ⟶ Cu²⁺ + 2·(N⁵⁺ + 3·O²⁻) + N²⁺ + O²⁻ + 2·H⁺ + O²⁻
Cu° + H⁺ + N⁵⁺ + 3·O²⁻ ⟶ Cu²⁺ + 2·N⁵⁺ + 6·O²⁻ + N²⁺ + O²⁻ + 2·H⁺ + O²⁻
Identificamos los elementos que se reducen y los que se oxidan. Recordar que si un elemento se reduce hay otro que se oxida.
El Cu° pasa a Cu²⁺, se oxida, cede 2 electrones.
El N⁵⁺ pasa a N²⁺, se reduce, capta 3 electrones.
Representamos la ecuación en forma iónica neta:
Cu° + N⁵⁺ ⟶ Cu²⁺ + N²⁺
Armamos las hemireacciones equilibradas:
![]()
Multiplicamos las hemirreacciones para que el número de electrones tomados o cedidos sea el mismo, luego sumamos.
![]()
Calculamos:
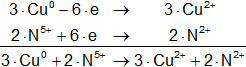
Volvemos a la primera ecuación y la armamos con los coeficientes hallados:
3·Cu + 2·HNO₃ ⟶ 3·Cu(NO₃)₂ + 2·NO + H₂O
Terminamos de equilibrar la ecuación por tanteo:
3·Cu + 8·HNO₃ ⟶ 3·Cu(NO₃)₂ + 2·NO + 4·H₂O
La ecuación queda igualada.
b) Reacción de oxidación del ion ferroso por el ácido nítrico con formación de ion férrico y óxido nítrico.
Fe(NO₃)₂ + HNO₃ ⟶ Fe(NO₃)₃ + NO + H₂O
Primero disociamos los compuestos detallando el número de oxidación:
Fe²⁺ + 2·(N⁵⁺ + 3·O²⁻) + H⁺ + N⁵⁺ + 3·O²⁻ ⟶ Fe³⁺ + 3·(N⁵⁺ + 3·O²⁻) + N²⁺ + O²⁻ + 2·H⁺ + O²⁻
Fe²⁺ + 2·N⁵⁺ + 6·O²⁻ + H⁺ + N⁵⁺ + 3·O²⁻ ⟶ Fe³⁺ + 3·N⁵⁺ + 9·O²⁻ + N²⁺ + O²⁻ + 2·H⁺ + O²⁻
Observamos que la suma algebraica de los números de oxidación de cada compuesto es cero.
Identificamos los elementos que se reducen y los que se oxidan. Recordar que si un elemento se reduce hay otro que se oxida.
El Fe²⁺ pasa a Fe³⁺, se oxida, cede 1 electrón.
El N⁵⁺ pasa a N²⁺, se reduce, capta 3 electrones.
Representamos la ecuación en forma iónica neta:
Fe²⁺ + N⁵⁺ ⟶ Fe³⁺ + N²⁺
Armamos las hemireacciones equilibradas:
![]()
Multiplicamos las hemirreacciones para que el número de electrones tomados o cedidos sea el mismo, luego sumamos.
![]()
Calculamos:
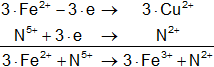
Volvemos a la primera ecuación y la armamos con los coeficientes hallados:
3·Fe(NO₃)₂ + HNO₃ ⟶ 3·Fe(NO₃)₃ + NO + H₂O
Terminamos de equilibrar la ecuación por tanteo:
3·Fe(NO₃)₂ + 4·HNO₃ ⟶ 3·Fe(NO₃)₃ + NO + 2·H₂O
La ecuación queda igualada.
c) Reacción de oxidación del cinc metálico por el ácido nítrico con formación de ion de cinc y dióxido de nitrógeno.
Zn + HNO₃ ⟶ Zn(NO₃)₂ + NO₂ + H₂O
Primero disociamos los compuestos detallando el número de oxidación:
Zn° + H⁺ + N⁵⁺ + 3·O ⟶ Zn²⁺ + 2·(N⁵⁺ + 3·O²⁻) + N⁴⁺ + 2·O²⁻ + 2·H⁺ + O²⁻
Zn° + H⁺ + N⁵⁺ + 3·O ⟶ Zn²⁺ + 2·N⁵⁺ + 6·O²⁻ + N⁴⁺ + 2·O²⁻ + 2·H⁺ + O²⁻
Observamos que la suma algebraica de los números de oxidación de cada compuesto es cero.
Identificamos los elementos que se reducen y los que se oxidan. Recordar que si un elemento se reduce hay otro que se oxida.
El Zn° pasa a Zn²⁺, se oxida, cede 3 electrones.
El N⁵⁺ pasa a N⁴⁺, se reduce, capta 1 electrón.
Representamos la ecuación en forma iónica neta:
Zn° + N⁵⁺ ⟶ Zn²⁺ + N⁴⁺
Armamos las hemireacciones equilibradas:
![]()
Multiplicamos las hemirreacciones para que el número de electrones tomados o cedidos sea el mismo, luego sumamos.
![]()
Calculamos:
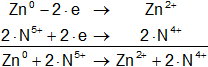
Volvemos a la primera ecuación y la armamos con los coeficientes hallados:
Zn + 2·HNO₃ ⟶ Zn(NO₃)₂ + 2·NO₂ + H₂O
Terminamos de equilibrar la ecuación por tanteo:
Zn + 4·HNO₃ ⟶ Zn(NO₃)₂ + 2·NO₂ + 2·H₂O
La ecuación queda igualada.
d) Reacción de oxidación del antimonio metálico por el ácido sulfúrico con formación de ion antimonioso y dióxido de azufre.
Sb + H₂SO₄ ⟶ Sb₂(SO₄)₃ + SO₂ + H₂O
Primero disociamos los compuestos detallando el número de oxidación:
Sb° + 2·H⁺ + S⁶⁺ + 4·O²⁻ ⟶ 2·Sb³⁺ + 3·(S⁶⁺ + 4·O²⁻) + S⁴⁺ + 2·O²⁻ + 2·H⁺ + O²⁻
Sb° + 2·H⁺ + S⁶⁺ + 4·O²⁻ ⟶ 2·Sb³⁺ + 3·S⁶⁺ + 12·O²⁻ + S⁴⁺ + 2·O²⁻ + 2·H⁺ + O²⁻
Observamos que la suma algebraica de los números de oxidación de cada compuesto es cero.
Identificamos los elementos que se reducen y los que se oxidan. Recordar que si un elemento se reduce hay otro que se oxida.
El Sb° pasa a Sb³⁺, se oxida, cede 3 electrones.
El S⁶⁺ pasa a S⁴⁺, se reduce, capta 2 electrones.
Representamos la ecuación en forma iónica neta:
Sb° + S⁶⁺ ⟶ Sb³⁺ + S⁴⁺
Armamos las hemireacciones equilibradas:
![]()
Multiplicamos las hemirreacciones para que el número de electrones tomados o cedidos sea el mismo, luego sumamos.
![]()
Calculamos:
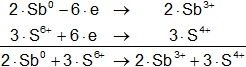
Volvemos a la primera ecuación y la armamos con los coeficientes hallados:
2·Sb + 3·H₂SO₄ ⟶ Sb2(SO₄)₃ + 3·SO₂ + H₂O
Terminamos de equilibrar la ecuación por tanteo:
2·Sb + 6·H₂SO₄ ⟶ Sb₂(SO₄)₃ + 3·SO₂ + 6·H₂O
La ecuación queda igualada.
e) Reacción de oxidación del ácido sulfhídrico por el ácido sulfúrico con formación de azufre libre.
H₂S + H₂SO₃ ⟶ S + H₂O
Primero disociamos los compuestos detallando el número de oxidación:
2·H⁺ + S²⁻ + 2·H⁺ + S⁴⁺ + 3·O²⁻ ⟶ S° + 2·H⁺ + O²⁻
Observamos que la suma algebraica de los números de oxidación de cada compuesto es cero.
Identificamos los elementos que se reducen y los que se oxidan. Recordar que si un elemento se reduce hay otro que se oxida.
El S²⁻ pasa a S°, se oxida, cede 2 electrones.
El S⁴⁺ pasa a S°, se reduce, capta 4 electrones.
Representamos la ecuación en forma iónica neta:
S²⁻ + S⁴⁺ ⟶ S°
Armamos las hemireacciones equilibradas:
![]()
Multiplicamos las hemirreacciones para que el número de electrones tomados o cedidos sea el mismo, luego sumamos.
![]()
Calculamos:
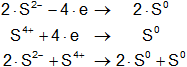
2·S²⁻ + S⁴⁺ ⟶ 3·S°
Volvemos a la primera ecuación y la armamos con los coeficientes hallados:
2·H₂S + H₂SO₃ ⟶ 3·S + H₂O
Terminamos de equilibrar la ecuación por tanteo:
2·H₂S + H₂SO₃ ⟶ 3·S + 3·H₂O
La ecuación queda igualada.
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP03
- | Siguiente ›
Ejemplo, cómo igualar ecuaciones redox