Problema nº 1 de estequiometría de las disoluciones, concentración de una disolución
Enunciado del ejercicio nº 1
Expresar la concentración de 40 g de una solución acuosa que contiene 8 g de soluto (st) y cuya densidad es de 1,15 g/cm³, en:
a) Gramos de soluto (st) por 100 g de solución (sc).
b) Gramos de soluto (st) por 100 g de disiolvente.
c) Gramos de soluto (st) por 100 cm³ de solución (sc).
Desarrollo
Datos:
Solución = 40 g
Soluto = 8 g
δ = 1,15 g/cm³
Fórmulas:
Solución
a)
El soluto forma parte de la solución.
Aplicamos regla de tres simple:
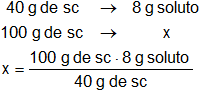
Resultado:
x = 20 g de soluto (st) por 100 g de solución
b)
Si la masa de la solución es de 40 g y la masa del soluto es de 8 g, entonces, la masa del disolvente es de 32 g.
Aplicamos regla de tres simple:
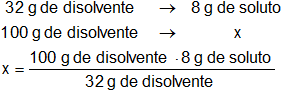
Resultado:
x = 25 g de soluto (st) por 100 g de disolvente
c)
Conocemos la masa de la solución, pero para hallar lo solicitado necesitamos el volumen de la solución.
Aplicamos la fórmula de densidad:
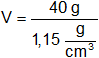
V = 34,783 cm³
Aplicamos regla de tres simple:
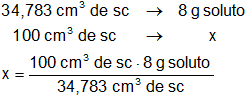
Resultado:
x = 23 g de soluto (st) por 100 cm³ de solución
Resolvió: Ricardo Santiago Netto. Argentina
Ejemplo, cómo calcular la concentración de una disolución