Problema nº 1 de estequiometría de las disoluciones, volumen y molaridad - TP07

Enunciado del ejercicio nº 1

¿Qué volumen de una disolución (sc) de ácido sulfúrico 1,4 M se necesita para reaccionar exactamente con 100 g de aluminio?

M₁ = 1,4 M

Molaridad (M): es el número de moles que tiene una solución por 1.000 cm³ de solución (sc).

La ecuación estequiométrica balanceada es la siguiente:

2·Al + 3·H₂SO₄ ⟶ Al₂(SO₄)₃ + 3·H₂

Calculamos las masas de los moles que intervienen en la reacción en equilibrio:

2·Al: 2·26,9815 g = 53,963 g

3·H₂SO₄: 3·(2·1,00797 g + 32,064 g + 4·15,9994 g) = 294,23262 g

Al₂(SO₄)₃: 2·26,9815 g + 3·(32,064 g + 4·15,9994 g) = 342,1478 g

3·H₂: 3·(2·1,00797 g) = 6,04782 g

La ecuación estequiométrica determina que 2 moles de Al se neutralizan con 3 moles de H₂SO₄.

A continuación, calculamos los moles de ácido sulfúrico puro necesaria para reaccionar con 100 g de aluminio:

Cálculo del número de moles en una solución

n = 5,55936475 moles de H₂SO₄

Determinados los moles de ácido sulfúrico puro necesaria calculamos el volumen.

Una solución 1,4 M de H₂SO₄ tiene 1,4 moles de ácido sulfúrico cada 1.000 cm³ de solución:

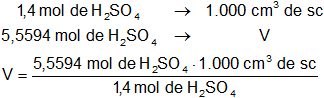
Cálculo del volumen en soluciones químicas

V = 3.970,974821 cm³ de solución

Resultado, el volumen de la disolución de ácido sulfúrico 1,4 M necesaria es:

V = 3.970,974821 cm³ = 3,97 dm³

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular el volumen utilizado de una disolución