Problema nº 8 de moléculas en la masa de una sustancia - TP08

Enunciado del ejercicio nº 8

Calcular el peso de una molécula de:

a) CH₃OH;

b) C₆₀H₁₂₂;

c) C₁₂₀₀H₂₀₀₀O₁₀₀₀

Desarrollo

Para hallar el valor de una molécula gramo o mol de una sustancia debemos conocer el valor de los pesos atómicos relativos de los átomos que la forman.

El mol es la suma de los pesos atómicos de todos los elementos que forman la molécula.

Solución

El número de Avogadro expresa el número de moléculas que hay en un mol de esa sustancia.

a) CH₃OH

Los pesos atómicos de los elementos presentes en el metanol son:

m_H = 1,00797 g

m_C = 12,01115 g

m_O = 15,9994 g

Multiplicamos por la cantidad de átomos presentes en la sustancia y sumamos:

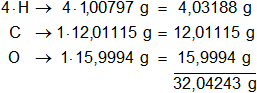
Mol = 32,04243 g de CH₃OH

Por lo tanto:

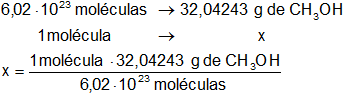
x = 5,323·10⁻²³ g de CH₃OH

Respuesta a), el peso de una molécula de CH₃OH es:

x = 5,323·10⁻²³ g

b) C₆₀H₁₂₂

Los pesos atómicos de los elementos presentes en el hexacontano son:

m_H = 1,00797 g

m_C = 12,01115 g

Multiplicamos por la cantidad de átomos presentes en la sustancia:

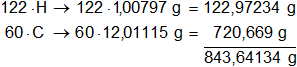
Mol = 843,64134 g de C₆₀H₁₂₂

Por lo tanto:

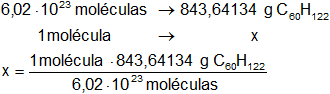
x = 1,401·10⁻²¹ g de C₆₀H₁₂₂

Respuesta b), el peso de una molécula de C₆₀H₁₂₂ es:

x = 1,401·10⁻²¹ g

c) C₁₂₀₀H₂₀₀₀O₁₀₀₀

Los pesos atómicos de los elementos presentes en el C₁₂₀₀H₂₀₀₀O₁₀₀₀ son:

m_H = 1,00797 g

m_C = 12,01115 g

m_O = 15,9994 g

Multiplicamos por la cantidad de átomos presentes en la sustancia y sumamos:

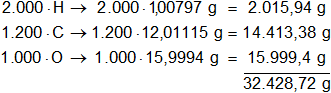
Mol = 32.428,72 g de C₁₂₀₀H₂₀₀₀O₁₀₀₀

Por lo tanto:

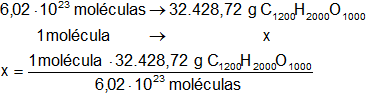
x = 5,387·10⁻²⁰ g de C₁₂₀₀H₂₀₀₀O₁₀₀₀

Respuesta c), el peso de una molécula de C₁₂₀₀H₂₀₀₀O₁₀₀₀ es:

x = 5,387·10⁻²⁰ g

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP08
• | Siguiente ›

Ejemplos de cómo calcular las moléculas que hay en mol