Superconductividad eléctrica (Parte II)
Propiedades de los Superconductores de Alta Temperatura
El resultado experimental más relevante, desde el punto de vista que nos ocupa, fue detectado por los propios descubridores de la superconductividad en los óxidos de cobre, Johannes Georg Bednorz y Karl Alexander Müller. Se trata de una característica importante de los SAT: La corriente crítica se anuLa para valores de campo notoriamente menores que Hc2(T). Por lo cual, el rango de campos y temperaturas donde los materiales podrían utilizarse es reducido. El progreso realizado en el conocimiento del comportamiento y naturaleza de los vórtices en los SAT ha permitido extender los rangos de T y H de aplicabilidad tecnológica, y descubrir notorias diferencias en el diagrama de fases H-T cuando es comparado con el de los superconductores convencionales.
En la figura 1 mostramos esquemáticamente el diagrama de fases de los superconductores convencionales (figura 1a) y el que se estimaba, hasta no hace mucho, correspondía a las características fundamentales de los SAT (figura 5).
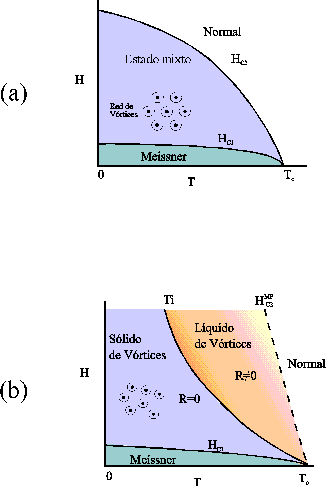
Figura 5. - Esquema del diagrama de fases H-T para: (a) superconductores convencionales (b) superconductores de alta temperatura.
Tal como dijimos, los superconductores convencionales tienen Jc 0 para todo campo y temperatura en el rango Hc1(T) < H < Hc2(T), ver figura 1a. En los SAT existe una zona de campos y temperaturas donde Jc = 0, separada por una línea bien definida de la zona donde Jc = 0. La línea de separación se ha llamado línea de irreversibilidad, Tᵢ(H), ver figura 1b.
Basándonos en lo discutido para los superconductores convencionales podemos describir la zona del diagrama de fases con Jc = 0 suponiendo que los centros de anclaje han perdido allí su efectividad. Es válido preguntarse si bajo esa circunstancia la estructura de vórtices recuperará el orden topológico de largo alcance para T > Tᵢ(H). En todo caso, no resulta trivial saber cuál es el mecanismo por el que el potencial de anclaje se anula.
Las primeras propuestas para alcanzar una compresión de las propiedades estáticas y dinámicas de los vórtices en los SAT, consistieron en extensiones y adaptaciones de mecanismos que tenían en cuenta los efectos de activación térmica en los superconductores tradicionales.
Las fuerzas de anclaje están asociadas a barreras de potencial de altura finita, que podrían ser sobrepasadas por los vórtices cuando son sometidos a efectos de activación térmica. Este proceso se puso en evidencia en los superconductores convencionales a través de la detección de fenómenos de "creep". Los estados metaestables asociados a los vórtices anclados evolucionan en el tiempo debido a que, a través de la activación térmica, un número finito de vórtices se salen de sus centros de anclaje. Al actuar sobre ellos la fuerza de Lorentz los vórtices se desplazan, dando origen a una resistencia eléctrica con una dependencia en temperatura típica de los procesos térmicamente activados. Del estudio experimental de las energías de activación se verificó que las barreras eran mucho más altas que la energía asociada a las temperaturas donde el material era superconductor. De hecho, las barreras de anclaje son tan altas, comparadas con los valores de energía térmica accesibles a los superconductores convencionales, que, a los efectos de las aplicaciones, los vórtices pueden considerarse anclados cuando J < Jc.
En contraposición con lo discutido para los superconductores convencionales, los fenómenos dependientes del tiempo, asociados a la estructura de vórtices de los SAT, son observables con mucha facilidad en amplios rangos de temperatura y dominan las propiedades dinámicas en las proximidades de Tᵢ(H). Pareció natural extender a los SAT los conocimientos que se habían obtenido a través del estudio de los fenómenos dependientes del tiempo en los superconductores convencionales. Para poder hacerlo fue indispensable encontrar razones que justificasen la existencia de potenciales efectivos, entre defectos y vórtices, con barreras de potencial notoriamente reducidas.
Las mediciones de Hc2(T) permitieron estimar la longitud de coherencia (0) 20 Å de los SAT. Este valor es, al menos, un orden de magnitud menor que los típicos para superconductores convencionales.
El potencial de anclaje asociado a la pérdida de energía e condensación de pares es proporcional a un volumen dado por 2(0) l, donde l es el largo efectivo del centro de anclaje.
La pequeña longitud de coherencia de los SAT sugiere el origen de características particulares de estos materiales:
- El potencial de anclaje se reduce en órdenes de magnitud. Esto, unido al acceso a temperaturas más altas, llevó a sugerir la existencia de un fenómeno de "creep" gigante
- Es razonable suponer que el "tamaño" de un par de Cooper debe ser igual o menor que (0). Teniendo en cuenta que (0) supera en poco el tamaño de la celda unidad atómica (13 Å) podemos concluir que el acoplamiento electrónico que da origen a la formación de pares en los SAT proviene de interacciones de corto alcance, comparado con el rango de interacción de largo alcance que asiste a la formación de pares en los superconductores convencionales
Las apreciaciones precedentes nos obligan a reconsiderar los rangos de aplicabilidad de las teorías de campo medio a la interpretación de la fenomenología de los SAT.
Las primeras tentativas dedicadas a explicar la existencia de Tᵢ(H) se basaron en considerar los efectos asociados a la existencia de un "creep" gigante. De existir esa importante activación térmica resulta razonable asociar Tᵢ(H) con la temperatura a la cual la mayoría de los vórtices se liberan de sus centros de anclaje. Sin embargo, la interpretación que hicieron Gammel et al. [1] de sus resultados en experimentos con la utilización de un oscilador mecánico distaba mucho de las ideas que sostenían los que abogaban por explicaciones basadas en fenómenos de activación térmica. [2] Ellos concluyeron que Tᵢ(H) representaba la temperatura donde tenía lugar una verdadera transición de fase, el paso de una red sólida a un líquido de vórtices [1].
La posibilidad de tener una fusión en la red de vórtices, similar a la que se observa en una red de átomos, no ha sido aceptada sin varios años de investigación e intensa controversia. Los que rebatían la posibilidad de una fusión, lo hacían basándose en los conceptos tradicionales que ya hemos discutido: La fusión implica un ablandamiento de las constantes elásticas y con ello una optimización del anclaje, con el consiguiente aumento de la corriente crítica, previo a la fusión de la red. Los que sostenían esta posición utilizaban concepciones asociadas a la forma convencional de tratar el anclaje, que considera que el estado fundamental de la estructura de vórtices es una red perfecta, perturbada por la presencia de centros de anclaje. Veremos que esta presunción es, en muchos casos, inadecuada para analizar los resultados experimentales obtenidos en los SAT.
Propuestas teóricas
Estimulados por las sugerencias de Gammel et al., algunos investigadores vislumbraron nuevas posibilidades teóricas para describir las propiedades estáticas y dinámicas de las estructuras de vórtices en los SAT. Una revisión de las primeras ideas y sugerencias estimativas de cómo se origina Tᵢ(H) fue presentada por Ronald Fisher, Fisher y Huse y un análisis más reciente de las diversas posibilidades se encuentra en la ref.
No vamos a detallar las aproximaciones hechas en la teoría, sólo puntualizaremos que provee un marco conceptual distinto al que se utiliza para los superconductores convencionales. Presenta una nueva visión del estado mixto, los vórtices no pueden tratarse independientemente del desorden inducido por el potencial de anclaje. Propone que el estado fundamental es un estado desordenado topológicamente, que denomina vidrio de vórtices. A diferencia del caso que hemos venido tratando, donde la red de vórtices se distorsiona por la perturbación inducida por potenciales de anclaje y la energía térmica induce reacomodamientos locales en la estructura de vórtices, el vidrio de vórtices trata en un mismo plano las interacciones vórtice-vórtice y vórtice-defecto, de tal forma que el estado fundamental resultante presenta desorden topológico y orden de largo alcance superconductor. En este nuevo estado la fase del parámetro de orden está bien definida y el paso de corrientes eléctricas se produce sin disipación. Es un estado de resistencia nula: el material se convierte en un verdadero superconductor.
De acuerdo con la teoría, la temperatura genera excitaciones del estado fundamental y en Tᵢ(H) se produce una transición de un estado sólido a un estado líquido de líneas de vórtices, incoherente en la dirección perpendicular al campo externo. El material se hace resistivo a través de una transición de fase de segundo orden. En este marco, la transición está dominada por las excitaciones asociadas a las fluctuaciones termodinámicas, que se ponen de manifiesto en la zona crítica. Tanto las propiedades termodinámicas como las de transporte quedan expresadas por reglas de escala con exponentes críticos.
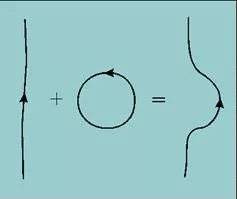
Figura 6: Representación de un vórtice distorsionado por las fluctuaciones térmicas como la adición de un vórtice toroidal a un vórtice a T = 0.
Es importante mencionar el tipo de excitaciones que aparecen en el estado de vidrio y que dan lugar a la existencia de la transición de fase contínua. Las excitaciones en el estado superconductor que cambian el orden asociado a la fase del parámetro de orden no pueden ser otras que vórtices. Sin embargo, ya se dijo que cambiar el número de vórtices que atraviesan la muestra implica excitaciones de energía muy alta. Una manera de introducir excitaciones en forma de vórtices, sin cambiar la magnetización termodinámica del material, es a través de vórtices que se cierran sobre sí mismos. Estas excitaciones con flujo magnético contenido en un toroide (ver figura 1) no cambian el número medio de vórtices y, por ende, no cambian la magnetización media, aunque pueden cambiar localmente el número de vórtices. La energía libre F de un vórtice cerrado sobre sí mismo, de radio r está dada por
| F = -π·r²·J· | Φ₀ | + 2·π·r·ε (1) |
| c |
Donde, F es la energía de línea del vórtice, calculada en la aproximación de G-L. Las excitaciones contribuyen a aumentar la entropía y la energía interna del sistema de vórtices.
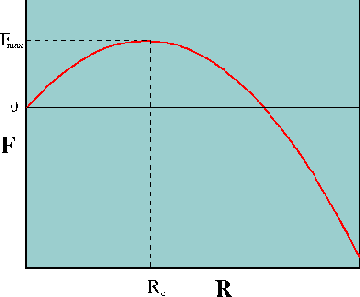
Figura 7. - Energía libre F de un vórtice toroidal como función de su radio r.
Es importante analizar qué efecto tienen las corrientes sobre las excitaciones. Si la corriente atraviesa el agujero del toroide de flujo, ejerce una fuerza de Lorentz. Esta fuerza tiende a expandir el toroide a expensas de aumentar su energía de línea. La energía resultante como función del radio presenta un máximo, tal como se ve en la figura 2. El radio correspondiente al máximo de la energía está relacionado con la corriente por:
| Rc = | ε·c | (2) |
| J·Φ₀ |
Si la corriente aplicada es menor que la asociada al máximo de la energía, el radio no crecerá y eventualmente la excitación podrá colapsar. Sin embargo, si la corriente excede la del máximo la excitación se expandirá. Este crecimiento o desplazamiento del vórtice implica disipación de energía.
Hay una diferencia fundamental entre el proceso de disipación que acabamos de describir a través de excitaciones del estado fundamental de vidrios de vórtices y aquel que se asocia al fenómeno de creep en los superconductores convencionales. En el primer caso el vórtice cambia su tamaño con la corriente aplicada; en el segundo el vórtice no cambia su estructura, solamente es desplazado por la fuerza ejercida por la corriente. En el primer caso la respuesta depende de la corriente aplicada, tal que para J0, R0, en el segundo la respuesta es lineal.
En equilibrio termodinámico habrá un cierto número de excitaciones, caracterizadas por su radio R, que se distribuyen entre los vórtices asociados al campo H. La población de radio mayor irá creciendo con temperatura y para una corriente dada aumentará la disipación. De acuerdo con la teoría en T = Tᵢ(H) el radio de las excitaciones diverge y se pasa a un régimen de disipación lineal.
De acuerdo a los fundamentos de la teoría que hemos presentado, tanto el vidrio de vórtices como el líquido de líneas tienen coherencia de fase superconductora en la dirección del campo. La transición de fase se refiere a la pérdida de simetría asociada a la destrucción del orden de largo alcance superconductor en la dirección perpendicular al campo.
La comparación de la teoría con los experimentos no es simple cuando hay que demostrar la existencia de reglas de escala. Es necesario determinar las propiedades físicas que ponen de manifiesto las fluctuaciones críticas con la precisión suficiente para verificar las reglas de escala en varios órdenes de magnitud de la variable que se analiza. Es pertinente notar que el acceso experimental a las propiedades del estado fundamental sólo se puede conseguir cuando se está en la zona de fluctuaciones críticas. Fuera de ella, la estructura de vórtices está en estados metaestables y su tendencia hacia el estado fundamental está limitada por tiempos característicos muy largos. Deducir las propiedades del estado fundamental a través de la evolución temporal de las cantidades físicas es un ejercicio difícil, con resultados dudosos en el mejor de los casos. Es por ello, que la verificación de la propuesta teórica para el estado fundamental debe realizarse a través de experimentos que accedan a la zona crítica.
Un buen número de experimentos han mostrado la existencia de transiciones de fase de segundo orden en Tᵢ(H). Aunque existen discusiones sobre la naturaleza del estado fundamental, pocos dudan de que el paso del comportamiento desde T < Tᵢ(H) a T > Tᵢ(H) se hace a través de una verdadera transición de fase donde se produce un cambio de simetría. Veremos en este artículo, sin embargo, que los resultados experimentales vuelven a mostrar la necesidad de reconsiderar la naturaleza misma de los vórtices en los superconductores de alta temperatura, y junto con ello la de la transición de fase.
Autor: Juan Augusto Arauz.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).