Superconductividad eléctrica (Parte III)

Desorden y transiciones de fase

La transición termodinámica superconductor-normal de los superconductores tradicionales en H_c2(T) es de segundo orden y está bien descripta por teorías de campo medio. La zona crítica donde dominan las fluctuaciones tiene un rango de temperaturas tan angosto que no es alcanzable a través de experimentos.

El rol de los defectos estructurales del material es importante porque ellos determinan la capacidad de transportar corriente sin disipación. Sin embargo su contribución a las propiedades termodinámicas del estado superconductor es nula: tanto la temperatura crítica como la energía de condensación no varían con la presencia de defectos.

Los campos H_c1(T) y H_c2(T) pueden cambiar con la densidad de defectos, a través de la dependencia de los parámetros superconductores (T) y (T) del camino libre medio electrónico. Como las constantes elásticas de la red de vórtices dependen de los parámetros superconductores y estos pueden cambiar con la concentración de defectos es comprensible que las propiedades elásticas de la red cambien de acuerdo al tipo y concentración de defectos que tenga el material. Si bien los campos críticos cambian con los defectos, y consecuentemente el diagrama de fases H-T, no cambia la naturaleza de la transición de fase en el correspondiente H_c2(T), que sigue siendo bien descripta por las teorías de campo medio.

Las corrientes críticas del material superconductor dependen de la capacidad de los defectos estructurales para controlar el anclaje de los vórtices. En 1.970 Larkin propuso la teoría de anclaje colectivo, en la cual los defectos de los materiales destruyen el orden cristalino de largo alcance de la red de vórtices. Esto ocurre como consecuencia de la competencia entre las interacciones entre vórtices y la energía que gana al situar a estos sobre los centros de anclaje. El aumento de la energía elástica de la red de vórtices, asociada a la deformación inducida por los centros de anclaje sobre la red, evita que estos optimicen la energía de interacción vórtice-defecto. Dentro de esa competencia y considerando la aproximación de Larkin, la estructura periódica no es estable, se pierde el orden de largo alcance y sólo quedan correlaciones posicionales de vórtices con orden de corto alcance. Estas correlaciones no deben ser confundidas con las correlaciones de fase que se discuten en este artículo. La correlación posicional se define, siguiendo a Larkin, como la distancia que se recorre a partir de un origen arbitrario para detectar que un vórtice se ha desplazado elásticamente en un parámetro de red. Como la red de vórtices admite desplazamiento en la dirección paralela y perpendicular al campo se define un volumen de correlación. El volumen de correlación lleva asociada una energía elástica, producto de la deformación inducida por los defectos. En la teoría queda implícito que cuando las deformaciones excedan el parámetro de red se inducirán deformaciones plásticas que relajan la energía de deformación. En la teoría de anclaje colectivo la corriente crítica es inversamente proporcional al volumen de correlación. El efecto de la temperatura se manifiesta a través del comportamiento de las constantes elásticas y los potenciales de anclaje.

La posibilidad de que existiesen transiciones termodinámicas en la estructura de vórtices en el estado mixto de los SAT, inducidas por fluctuaciones térmicas, impulsó un enfoque completamente distinto del problema. En ese nuevo enfoque los defectos juegan un papel importante, de tal suerte que el estado fundamental de la estructura de vórtices queda determinado por el efecto combinado de la interacción vórtice-vórtice y vórtice-defecto. La teoría justifica la existencia de una transición de fase de segundo orden que separa un estado sólido a bajas temperaturas de un estado líquido a temperaturas mayores y predice la existencia de una zona crítica, donde las fluctuaciones determinan las propiedades físicas del sistema. Esta zona crítica es lo suficientemente amplia como para tener acceso a ella a través de experimentos. Los resultados experimentales verificaron la existencia de exponentes críticos y comprobaron que la descripción correcta del comportamiento fenomenológico de los SAT debía hacerse dentro de una teoría que fuese más allá de las limitaciones impuestas por aquellas basadas en la aproximación de campo medio.

Los experimentos de nuevo pusieron de manifiesto otros fenómenos peculiares de los SAT al descubrir que, dependiendo del tipo de defectos, existían transiciones de primer orden para el paso de líquido a sólido en la estructura de vórtices. Las primeras evidencias fueron reforzadas a través de nuevas mediciones de transporte, difracción de neutrones y magnetización en más de un superconductor de alta temperatura. No existe hasta ahora ninguna teoría que describa la transición de fase de primer orden.

Terminamos esta sección puntualizando las diferencias fundamentales entre los volúmenes de correlación que se describen en la teoría de Larkin y las correlaciones de fase que determinamos al hacer los experimentos con el transformador de corriente contínua descriptos en este artículo. El volumen de correlación de Larkin surge de un análisis topológico de la distribución espacial de los vórtices. De hecho se basa en suponer que el estado fundamental es una red periódica de vórtices que se modifica por la presencia de defectos. Las fuerzas de anclaje actúan sobre constantes elásticas bien definidas que caracterizan la red periódica. En este tratamiento se da por sentado que la coherencia de fase se establece en volúmenes mayores que el volumen de Larkin: no se pueden definir constantes elásticas de la "red" superconductora en volúmenes en que no haya correlación de fase. De hecho, para corrientes menores que la crítica, en la imagen de Larkin, el volumen de correlación de fase es infinito.

Después de varios años de investigación y controversias se acepta que las características del estado mixto de los superconductores de alta temperatura, SAT, difieren cualitativamente de aquellas de los superconductores convencionales, SC. Las diferencias se ponen de manifiesto no sólo en aspectos cuantitativos asociados a valores particulares de los parámetros superconductores, sino a través de diferencias cualitativas en sus propiedades físicas e interpretaciones teóricas.

Como consecuencia, los superconductores basados en óxidos de Cu deben tratarse en un marco diferente al que proveen teorías de campo medio.

El comportamiento diferente de los SAT se debe al efecto combinado de su pequeña longitud de coherencia, (T), la relevancia de la contribución de fluctuaciones termodinámicas del parámetro de orden, y su gran anisotropía.

Después de aceptarse la existencia de una transición de fase termodinámica que separa una fase líquida de vórtices de una estructura sólida, se descubrió que el diagrama de fases H-T del estado mixto es más rico que lo que se creía en ese momento. Se determinó que la transición de líquido a sólido en muestras monocristalinas sin maclas, denominadas limpias, de YBa₂Cu₃O₇- (YBCO) es una transición termodinámica de primer orden que ocurre a lo largo de una línea Tₘ(H) en el diagrama H-T. La presencia de maclas, muestras sucias, transforma la transición de primer orden en una de segundo, a la temperatura Tᵢ(H).

Llama la atención que la estructura de vórtices de muestras limpias, tanto de YBCO (considerado como un SAT de moderada anisotropía, con un cociente de masas de 50) como de Bi₂Sr₂CaCu₂O₈ (BSCCO) (con > 104), presente la transición de primer orden termodinámico. El papel relevante que juega la anisotropía en los SAT, al permitir que las fluctuaciones térmicas sean importantes en las propiedades termodinámicas, es reconocido. Sin embargo, no es fácil comprender por qué variaciones de la anisotropía en varios órdenes de magnitud no cambian la naturaleza de la transición de fase líquido-sólido, cuando sí lo hace la presencia del desorden topológico introducido por las maclas en YBCO. En consecuencia, es importante preguntarse qué papel desempeña el desorden topológico y cómo compite con la anisotropía de los superconductores para cambiar cualitativamente el diagrama de fases del estado mixto.

Las mediciones de transporte utilizando la configuración de contactos del transformador de corriente contínua son de particular importancia en el estudio de la correlación de la fase superconductora en la dirección del eje c cristalográfico (consideramos al campo magnético aplicado en la dirección c). Usaremos los datos provistos por esta técnica para realizar un estudio comparativo de las funciones de correlación de la fase del parámetro de orden en muestras con maclas y libres de ellas. La técnica experimental utilizada y las características de las muestras han sido descritas en varias publicaciones.

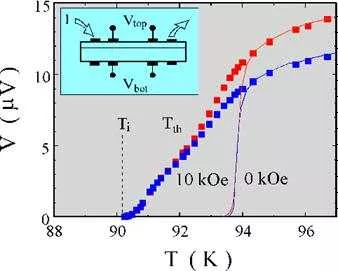
Figura 8. Resultados típicos del voltaje en la cara superior e inferior de una muestra cristalina de YBCO, Vₜₒₚ y V_bot, en función de temperatura. La distribución de contactos eléctricos correspondientes al transformador de corriente contínua se indica esquemáticamente en la figura. Los datos corresponden a la transición sin campo aplicado y con un campo magnético paralelo al eje c de 10.000 Oe

En la figura 1 se muestran resultados de mediciones de voltaje a corriente constante en función de temperatura, utilizando la configuración del transformador, en muestras monocristalinas de YBCO con maclas. La configuración de contactos se puede ver en la misma figura. El campo aplicado es en este caso 10 kOe. Los voltajes se inducen con corrientes lo suficientemente bajas para asegurar respuesta lineal.

Los resultados muestran que la transición de segundo orden de líquido a sólido en Tᵢ(H) va acompañada de la consabida disipación (resistencia finita) en el plano ab y que los voltajes en la cara superior (Vₜₒₚ) y en la cara inferior (V_bot) coinciden para temperaturas superiores a Tᵢ(H). Al alcanzar una temperatura Tₜₕ(H) se observa que Vₜₒₚ V_bot. Esta diferencia aumenta con temperatura y persiste al alcanzar el estado normal en T = T_c. Para T > T_c la diferencia de voltajes queda determinada por la distribución inhomogénea de corrientes asociada a la configuración de contactos utilizada y la resistividad del material en el estado normal.

La diferencia entre los voltajes de la cara superior e inferior de la muestra, en el rango de temperaturas Tₜₕ < T < T_c, indica que el sistema es disipativo en el eje c. Teniendo en cuenta que los datos se toman en el régimen de respuesta lineal concluimos que la resistencia en las direcciones ab y c es una propiedad intrínseca, no inducida por la presencia de la corriente. En este sentido podemos asegurar que para T > Tₜₕ(H) el líquido de vórtices pierde la correlación de fase en todas las direcciones: no hay superconductividad (no hay estado de resistencia nula). Los resultados muestran que la presencia de una densidad finita de pares de Cooper e incluso la presencia de vórtices no implican superconductividad. Es importante preguntarse si hay una o dos temperaturas a las cuales se establece la superconductividad.

Es fácil interpretar el resultado Vₜₒₚ = V_bot en el rango Tᵢ(H) < T < Tₜₕ(H) en términos de la respuesta del transformador cuando se ejercen fuerzas inhomogéneas sobre líneas de vórtices (vórtices con correlación de fase a través de la muestra en la dirección del campo). En el régimen estacionario el número de vórtices que pasan entre los contactos de la cara superior e inferior es el mismo, con lo cual Vₜₒₚ = V_bot. Si se incrementa la corriente de medición se induce el corte de vórtices, se pierde la coherencia de fase, Vₜₒₚ V_bot. Queda así demostrada la existencia de fuerzas inhomogéneas en la configuración utilizada, aun en el caso en que haya coherencia de fase en la dirección c. Vemos que Tₜₕ(H) es la temperatura a partir de la cual los vórtices pierden coherencia en la dirección del campo. En un lenguaje similar al que se usa para los polímeros decimos que la estructura de vórtices para T > Tₜₕ(H) corresponde a un sistema de líneas entrelazadas, con probabilidad finita de que se produzcan cortes entre ellas. Si la probabilidad de cortes entre vórtices es tal que se forma un camino de percolación en la dirección ab (formado por segmentos de vórtices entre cortes), se perderá la coherencia de fase en la dirección c y se producirá disipación, ver figura 2. Esta última interpretación ha sido sugerida y utilizada por Jagla y Balseiro para describir las transiciones de fase de segundo orden en la dirección c como transiciones de percolación bidimensional en la dirección ab.

Figura 9. Dibujo esquemático que representa el entrelazamiento y corte entre vórtices. En color rojo se indica el camino de percolación formado por segmentos de vórtices entre cortes. Cuando el camino de percolación se propaga de lado a lado de la muestra en la dirección ab se pierde la coherencia de fase en la dirección c.

Como resultado de la discusión anterior concluimos que existe un estado sólido por debajo de Tᵢ(H) con coherencia de fase en todas direcciones. En el rango Tᵢ(H) < T < Tₜₕ(H) existe una fase líquida de líneas de vórtices, sin coherencia superconductora en la dirección ab, y se mantiene la superconductividad en la dirección c. Cuando T > Tₜₕ(H) no hay superconductividad en la muestra. Los experimentos que discutimos no nos permiten dilucidar si la pérdida de superconductividad en Tₜₕ(H) se hace a través de una transición de fase o de un cambio de régimen. Teniendo en cuenta que se ha demostrado que en Tᵢ(H) se funde la estructura de vórtices con una transición de fase de segundo orden, es importante saber si la pérdida de superconductividad tiene lugar mediante dos transiciones de fase o una y, en este último caso, a qué corresponde el cambio de régimen en Tₜₕ(H).

En la figura 9 hemos graficado las dos líneas Tᵢ(H) y Tₜₕ(H) que delimitan las zonas del espacio H-T, donde se encuentran los distintos comportamientos del estado superconductor. Este diagrama H-T pone en evidencia que la descripción tradicional de que la pérdida de superconductividad se hace con una única transición de fase (de segundo orden termodinámico en H_c2(T)) debe ser modificada. El estado normal se alcanza para T > Tₜₕ(H), muy por debajo del valor de H_c2(T) provisto por teorías de campo medio.

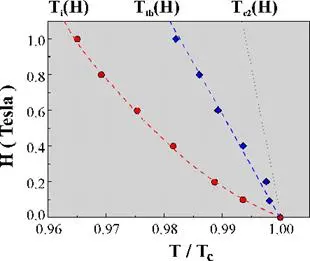
Figura 9. Diagrama de fases H-T para el estado mixto en una muestra cristalina de YBCO con maclas. La línea Tᵢ(H) corresponde a la transición de segundo orden que separa la fase sólida de la líquida de líneas de vórtices correlacionadas en la dirección c. El líquido de vórtices está decorrelacionado en todas direcciones para temperaturas mayores a la delimitada por Tₜₕ(H).

Antes de discutir cuáles son las propiedades que deben caracterizar las transiciones de fase, es importante profundizar el análisis de los resultados experimentales. La detección de Tₜₕ(H) a través de la medición de la temperatura a la cual Vₜₒₚ = V_bot es equivalente a determinar la temperatura en que la longitud de correlación de fase del vórtice en la dirección c, l(T, H), coincide con el espesor de la muestra, d. Esto es, en Tₜₕ(H) se cumple l(T, H) = d. Es por ello fundamental conocer si l(T, H) es una función contínua de T para un H constante, que crece cuando disminuye T, o es una función discontínua que caracteriza el paso de un estado desordenado a un estado de coherencia de fase con orden de largo alcance. En el primer caso Tₜₕ será función del espesor, en el segundo Tₜₕ(H) resultará independiente del espesor. Las mediciones con la configuración del transformador se extendieron a muestras de distintos espesores, poniendo en evidencia que en las muestras con maclas Tₜₕ(H) es función del espesor, tal como se ve en la figura 10a.

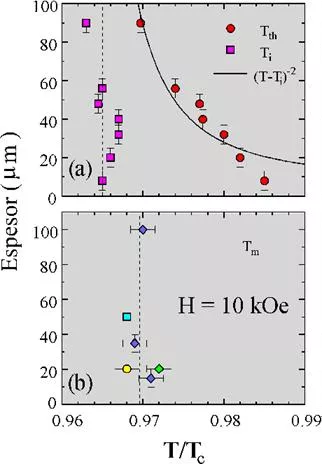
Figura 10. (a) Temperaturas Tₜₕ(H) y Tᵢ(H) en función del espesor de monocristales de YBCO con maclas. La línea contínua representa la dependencia en temperatura de la longitud de corte para una transición de Bose, ver texto. (b) Temperatura de fusión Tₘ(H) para la transición de primer orden en muestras de YBCO libres de maclas.

Safar et al. demostraron que las características de la transición sólido-líquido dependen del grado de desorden de las muestras.

Mediante cuidadosas mediciones de la resistencia eléctrica en el plano ab demostraron que la transición de segundo orden en Tᵢ(H) se transformaba en una de primero en Tₘ(H) cuando las muestras no tenían maclas. Teniendo en cuenta que las maclas cambian la naturaleza de la transición termodinámica sólido-líquido y que este cambio se detectó mediante mediciones de transporte que sólo censaban el comportamiento de la fase superconductora en la dirección ab, es importante preguntarse si la coherencia de fase en la dirección c sigue estableciéndose a una temperatura Tth Tm. Para responder esta pregunta se realizaron experimentos utilizando la configuración del transformador en muestras sin maclas.

Resultados típicos del voltaje en función de temperatura a corriente constante para muestras libres de maclas se muestran en la figura 5, para un campo de 40 kOe. En la misma figura se han graficado los resultados para la misma configuración de contactos en una muestra con maclas. Para facilitar la comparación se ha graficado Rₜₒₚ = Vₜₒₚ/I y R_bot = V_bot/I, donde I es la corriente de medición y se han normalizados los valores de R por Rₜₒₚ(T_c). Los datos se muestran en función de temperatura reducida para corregir los efectos de los pequeños cambios de temperatura crítica entre muestras.

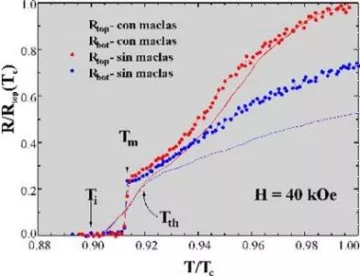
Figura 11. - Resistencia normalizada en función de temperatura reducida comparando el comportamiento de muestras monocristalinas de YBCO con y sin maclas utilizando la configuración de contactos del transformador de corriente contínua. Las flechas indican las temperaturas de transición discutidas en el texto.

Los resultados de la figura 5 ponen de manifiesto las principales diferencias entre las muestras macladas y las libres de esos defectos. Tal como se había observado en las mediciones de transporte con corriente uniforme la transición al estado sólido en las muestra sin maclas es abrupta, a una temperatura Tₘ(H). Es evidente que en ese tipo de muestras la transición de fusión detectada por la variación brusca de la resistencia en los planos coincide con la temperatura donde se establece la correlación de fase en la dirección c. En este tipo de materiales Tᵢ(H) = Tₜₕ(H) = Tₘ(H). El sólido de vórtices corresponde al estado correlacionado en todas direcciones y se transforma a través de la transición de primer orden en un líquido decorrelacionado en todas direcciones. La fase líquida desenredada, usando el lenguaje de Nelson, ha desaparecido, cuando se compara con lo observado en las muestras con maclas.

El resultado discutido anteriormente es relevante para comprender el comportamiento y respuesta de la estructura de vórtices ante la presencia de desorden introducido por defectos del material. Vemos así que la transición de primer orden caracteriza el comportamiento del material "limpio" y que en ella se pierde la correlación de la fase superconductora en todas las direcciones. En ese sentido, en las muestras sin maclas se pasa simultáneamente de un sólido correlacionado en todas direcciones a un líquido decorrelacionado tanto en la dirección c como en la ab. Este es un dato importante al que se tuvo acceso gracias a la medición de las propiedades de transporte inyectando distribuciones de corriente no uniformes.

Con la finalidad de profundizar la comparación del comportamiento de las muertas con maclas y sin ellas se hicieron mediciones de Tₘ(H) para muestras de distinto espesor. En este caso los resultados muestran que la transición ocurre a una sola temperatura, independiente del espesor de la muestra (ver figura 4b). Este resultado prueba que mientras que la transición de un sistema correlacionado de líneas de vórtices a un sistema decorrelacionado en la dirección del campo es una transición contínua en la muestras con maclas, se convierte en una discontínua en las muestras sin maclas. Los resultados experimentales implican que la naturaleza microscópica de la transición cambia fundamentalmente en función del tipo de desorden.

El hecho de que la presencia de desorden en la estructura atómica modifique el carácter de una transición termodinámica y la naturaleza misma de los vórtices es un fenómeno nuevo que caracteriza las propiedades de los SAT. De nuevo, la descripción tradicional del efecto del desorden estructural sobre las propiedades de los vórtices resulta inadecuada. Los defectos topológicos estructurales no pueden tratarse como perturbaciones sobre una red perfecta de vórtices cuyo único efecto sea anclar la red a la estructura atómica. Los defectos modifican la naturaleza de los vórtices al cambiar su función de correlación en la dirección del campo. Los resultados experimentales nos sugieren que las maclas establecen la coherencia de fase del vórtice a lo largo de su núcleo y que, una vez establecida, actúan sobre el vórtice tratando de anclarlo dentro del potencial generado por la presencia del defecto.

Las maclas pertenecen a una clase de defectos denominados correlacionados que han jugado un papel muy importante en la superconductividad de alta temperatura. La introducción de defectos columnares creados por irradiación de monocristales con iones pesados fue un paso fundamental para demostrar que se podía hacer crecer en órdenes de magnitud la corriente crítica en los SAT, paso esencial para poder pensar en posibles aplicaciones. Los defectos columnares son defectos correlacionados en una dimensión, a diferencia de las maclas que lo son en dos dimensiones. Antes de realizarse los experimentos que hemos discutido en este artículo se utilizaban los conceptos tradicionales de anclaje de vórtices en superconductores convencionales para explicar el aumento de corriente critica: el vórtice, tomado como línea, se ancla dentro del potencial correlacionado. Los resultados discutidos aquí muestran que el rol de los defectos correlacionados es más importante: "crean" las líneas y después las anclan.

En función de los datos analizados es conveniente finalizar este artículo reflexionando sobre propiedades que determinarían el origen microscópico de la transición o transiciones de fase, relacionadas con la pérdida de correlación de fase u orden de largo alcance en la dirección del eje c.

Para las muestras macladas los resultados indican que la coherencia de fase se establece cuando el espesor de la muestra coincide con la longitud de correlación. Podría pensarse que establecer correlación en el eje c corresponde a una transición de fase frustrada por la dimensión finita de la muestra. En este caso la transición para una muestra infinita correspondería a una longitud que diverge a alguna temperatura inferior a las determinadas experimentalmente, posiblemente coincidente con Tᵢ(H). Teniendo en cuenta el carácter correlacionado de los defectos esto correspondería a la transición de un gas de Bose bidimensional En este caso el gráfico de la figura 4a puede reinterpretarse como la dependencia en T de la función l(T, H), con una divergencia en Tᵢ(H). En la figura hemos graficado la dependencia en temperatura de l(T, H) de acuerdo con los autores de la ref. 13. La precisión de los datos experimentales no permite confirmar ni desmentir la teoría. Por otra parte Jagla y Balseiro han predicho a través de simulaciones numéricas y argumentos de plausibilidad, que la transición en Tₜₕ(H) es una transición de fase para un sistema pseudo-bidimensional, que depende del espesor de la muestra. En esta teoría la transición termodinámica se asocia a una transición percolativa de los segmentos de vórtices entre cortes, en la dirección ab. En Tₜₕ(H) el tamaño del cluster percolativo diverge. Es razonable pensar que Tₜₕ(H) dependa del espesor de la muestra, pues cuanto mayor sea la longitud de los vórtices más fácil será encontrar caminos percolativos y más baja la temperatura de percolación. La teoría predice la existencia de exponentes críticos con valores aproximados a los observados experimentalmente.

En el caso de la transición de primer orden la incertidumbre con respecto al origen microscópico de la transición de fase es mayor. La independencia de Tₘ(H) del espesor de la muestra ha sido verificada hasta un espesor mínimo de 15µm. Solamente podemos asegurar que el colapso de la longitud de correlación en Tₘ(H) es a valores menores que 15µm. Si bien este resultado es muy útil para caracterizar el efecto causado por la transición de primer orden en la pérdida de coherencia en la dirección del campo, no cubre el rango de espesores necesarios para proveer información que determine cual es la longitud de correlación de fase, l(T, H), en el eje c en Tₘ(H). Diseñar algún experimento que pueda determinar esa longitud es de suma importancia para verificar cualquier modelo teórico que intente describir la transición de fase a partir del elemento de coherencia determinado por el "vórtice elemental". Ese elemento no puede tener longitud menor que el espesor determinado por las capas de Cu-O.

La física de la transición de primer orden cambia de acuerdo a la longitud de correlación que se detecte en Tₘ(H). Si l(T, H) es la distancia entre planos de Cu-O se estaría en presencia de una transición de desacople entre planos. En este caso la energía térmica sería del orden de la energía Josephson que determina la coherencia entre planos. Si l(T, H) es mayor que la distancia mencionada estaríamos en presencia de una transición de primer orden de un líquido enredado de vórtices a un sólido de líneas. En este caso Tₘ(H) debería depender del espesor y para espesores suficientemente pequeños la transición de fase se transformaría en un cambio de régimen o en una transición del tipo bidimensional descrita anteriormente.

Hemos discutido aspectos conceptuales de sólo algunos de los problemas que presenta una nueva forma de materia condensada, constituida por los vórtices superconductores en los SAT, sus interacciones y la presencia de distintos tipos de defectos. A diferencia de lo que se aceptaba en los superconductores convencionales las fluctuaciones termodinámicas son esenciales para comprender sus propiedades y los defectos no actúan solamente como centros de anclaje sino que hay que incorporarlos al sistema de vórtices pues determinan sus características estructurales. Existen nuevas transiciones de fase que dan lugar a un variado y rico diagrama de fases. Más y nuevos experimentos en conjunto con el trabajo teórico permitirán en el futuro describir formalmente el comportamiento fenomenológico de la nueva superconductividad.

Técnicas experimentales

Muchos de los fenómenos físicos tratados en este artículo se manifiestan en propiedades magnéticas o de transporte eléctrico de los materiales superconductores. El estado Meissner en muestras masivas, por ejemplo, se caracteriza por el diamagnetismo perfecto (propiedad magnética) y la resistividad lineal nula (propiedad de transporte). En este anexo se da una breve reseña de algunas técnicas experimentales usadas para estudiar estas propiedades. También se describe una técnica de transporte, llamada transformador de flujo dc, que ha sido de gran utilidad en los últimos años para investigar la correlación de la fase superconductora en la dirección del campo magnético en el estado mixto de los SAT. Los resultados de esta técnica concentran la atención de la mayor parte de este artículo.

La magnetización M (H, T) del superconductor se debe a que las corrientes de apantallamiento del campo externo, que circulan en la superficie de la muestra, generan un momento magnético. En un campo estático, la dependencia de M (H, T) con el campo, la temperatura y el tiempo da información sobre la existencia de efecto Meissner, la penetración de flujo debida a los vórtices, la presencia, intensidad y carácter del anclaje de los vórtices, y otras propiedades. Al campo estático puede superponérsele un campo magnético oscilatorio y estudiar la respuesta del superconductor (susceptibilidad) (H, T), la cual permite investigar aspectos de la dinámica de las estructuras de flujo.

En el estado Meissner es posible sostener corrientes superconductoras de transporte (en el volumen de la muestra) sin disipación de energía. En presencia de vórtices, sin embargo, la corriente aplicada ejerce una fuerza de Lorentz sobre las líneas de flujo; si esta supera la de anclaje los vórtices se mueven y aparece un voltaje en la dirección de la corriente. La forma más simple de medir este voltaje es inyectar corriente por dos electrodos y conectar un voltímetro a otros dos terminales colocados en la línea que une los contactos de corriente. Las numerosas complicaciones que aparecen para aplicar esta técnica sencilla a monocristales de los SAT se deben a características propias de estos materiales que hacen difícil la realización de contactos de alta calidad y al hecho de que casi siempre se desea obtener gran sensibilidad a pequeños voltajes manteniendo la temperatura de la muestra bien controlada, en amplios rangos de campo magnético y temperatura.

Los contactos de los electrodos deben ser de baja resistencia para minimizar el ruido térmico y para evitar calentamiento local de joule al aplicar corriente. Una dificultad que se presenta para lograrlo es que el área disponible para fabricarlos es muy reducida: los monocristales comúnmente disponibles de los SAT son de dimensiones típicas de 1 mm² en la dirección de los planos ab y algunas decenas de micrones en la dirección c. Otro problema es la generación de una interfaz adecuada entre el superconductor y el material con el que se fabrica el electrodo. Las formas de obtener contactos de baja resistencia son numerosas. Una disposición que da buenos resultados en monocristales de YBCO consiste en formar para cada electrodo una "pista" de oro depositado por evaporación de unos 5.000 Å de espesor, la cual se somete a un tratamiento térmico (aproximadamente 8 h a una temperatura de 400 °C) para inducir la difusión del oro en la superficie de la muestra (este recocido debe hacerse en flujo de oxígeno gaseoso para evitar la desoxigenación del YBCO). Sobre la "pista" se adhiere después un trozo alambre de oro con un epoxy de plata que se endurece exponiéndolo a 100oC durante una hora. Las resistencias de contacto así obtenidas son del orden de 1 a temperatura ambiente.

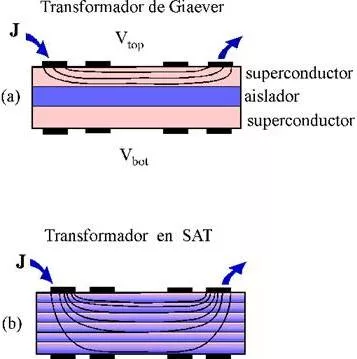
Figura 12. Distribución de contactos eléctricos para el transformador (a) de Giaever y (b) en un monocristal de SAT.

En 1.965 Ivar Giaever diseñó un experimento de transporte eléctrico que constituyó una de las pruebas más concluyentes de que la resistencia en el estado mixto de los superconductores del tipo II se origina en el movimiento de vórtices. La Figura 1a muestra un esquema de la disposición que empleó: se inyecta corriente en una lámina de estaño de 1.000Å de espesor ("primario") separada de otra lámina similar por una capa aislante de SiO de 200 Å de espesor. Con un campo magnético perpendicular a las láminas y a temperatura suficientemente baja se tienen vórtices en ambas láminas de estaño; las corrientes de los vórtices tienen una interacción magnética que los acopla a través del aislador.

Así, la corriente aplicada al "primario" ejerce fuerza sobre los vórtices de esa lámina los cuales, por intermedio de la interacción magnética, hacen fuerza sobre los del "secundario". Al moverse los vórtices del primario arrastran a los del secundario que, en el estado estacionario, se mueven con igual velocidad. De esta manera se mide un voltaje en el primario igual al del secundario, Vₜₒₚ = V_bot. El nombre de transformador de flujo a corriente contínua que se dio a la configuración usada por Giaever se debió a este resultado. Es obvio que en el estado normal, T > T_c el resultado experimental indicará Vₜₒₚ V_bot = 0.

Debido a la anisotropía de los SAT y a la importancia de las fluctuaciones térmicas, podría esperarse que la correlación de velocidades de los vórtices se pierda en distancias tales como los espesores típicos de las muestras. Para estudiar esto se puede extender la idea del experimento de Giaever a un monocristal de un SAT, tal como se muestra en la figura 1b. Se requieren dos electrodos de corriente y dos de voltaje en una cara (top) de un cristal en forma de lámina y dos electrodos de voltaje en la otra cara (bot) (normalmente se colocan electrodos de corriente en ambas caras para verificar la simetría de los resultados).

Se inyecta corriente por el top y se miden los voltajes Vₜₒₚ y V_bot. En este caso la corriente se distribuye a través de la muestra pero debido a la anisotropía (c > ab) y a la ubicación de contactos se tiene una distribución inhomogénea de corriente que hace que la fuerza de Lorentz ejercida sobre un vórtice sea máxima cerca de la cara superior y disminuya hacia abajo. Esta inhomogeneidad de la fuerza aplicada, presente en un cristal homogéneo por efecto de la distribución inhomogénea de corriente, permite estudiar la correlación de los vórtices en la dirección del campo aplicado mediante la comparación de los voltajes top y bot. En efecto, la técnica ha permitido determinar que en el compuesto BiSrCaCuO los vórtices son entidades cuasi-bidimensionales, sin correlación en la dirección del campo, en un amplio rango de temperaturas y campos magnéticos, mientras que en YBaCuO, menos anisotrópico, se tiene movimiento correlacionado de vórtices en una porción del diagrama de fases H-T, tal como se discute en este artículo.

Caracterización de sustratos para superconductores Y-123

Se han caracterizado [1] las perosquitas ordenadas Ba₂(RSb)O₆, (R Y, Ho), que son buenos sustratos para películas delgadas de YBa₂Cu₃O₇-. Con datos de difracción de neutrones en muestras policristalinas, se ha refinado la estructura de estas perosquitas en el grupo F mm (N° 225), con Z = 4, Ba en 8(c), R en 4(b), Sb en 4(a), y oxígeno en 24(e), obteniendo un parámetro de posición x = 0·2.636(2) para R = Y y Hₒ, y dimensiones de la celda unidad a = 8·4.240(3) y 8·4.170(2) para R = Y y Hₒ respectivamente. Se ha medido la susceptibilidad magnética de ambas perosquitas entre 2 y 350 K. La susceptibilidad paramagnética y su variación con la temperatura se han calculado según el formalismo de John Hasbrouck Van Vleck, a partir de una estimación a priori de los parámetros del campo del cristal correspondientes a la simetría de la posición de la tierra rara, Oh, y usando las funciones de onda asociadas con los niveles de energía obtenidos. La desviación observada respecto al comportamiento Curie-Weiss a baja temperatura, muy bien reproducida, refleja el desdoblamiento del estado normal del catión por influencia del campo.

Crecimiento de cristales superconductores y medida de sus propiedades

Se han crecido cristales de Bi-2.212, en los que se han estudiado los efectos de la fluctuación térmica sobre la magnetización, por encima y por debajo de la temperatura de transición superconductora, en el límite del campo magnético débil [1]; la influencia de pequeñas inhomogeneidades del contenido de oxígeno, sobre la paraconductividad y la magnetoconductividad inducida por fluctuación [2]; y los cambios discretos, a temperaturas cercanas a la crítica, en el infrarrojo lejano, de áreas de bandas de fonones en primer y segundo orden [3].

También se han crecido cristales de la espinela superconductora LiTi₂O₄, en la que se están realizando medidas para determinar la línea de irreversibilidad.

Estabilidad térmica de cupratos superconductores con oxoaniones

Se estudia la efecto de la sustitución parcial de Cu [1] por algunos grupos oxoaniones (SO₄²⁻, PO₄²⁻ y BO₃³⁻) en las propiedades de óxidos superconductores 1.212. La estabilidad térmica de los óxidos sustituidos disminuye en el orden BO₃³⁻ > PO₄²⁻ > SO₄²⁻, tal como indican las temperaturas de fusión peritéctica de los materiales sustituidos. Además, la sustitución por iones SO₄²⁻ y PO₄²⁻ hace variar la T_c desde 80 K para los materiales sin dopar, hasta 70 y 60 K para el oxosulfato y oxofosfato, respectivamente, mientras que la incorporación de iones BO₃³⁻ elimina la superconductividad.

Preparación y estudio de cupratos con estructura en capas infinitas

La llamada "estructura en capas infinitas" deriva de la perovskita ABO₃ al suprimir los oxígenos axiales de todos los grupos octaédricos. Los cupratos de estequiometria (Sr, Ca)CuO₂ presentan dicha estructura, que se ha de estabilizar a alta presión hidrostática. Se ha descrito superconductividad en materiales dopados con huecos o electrones. Con una prensa hidrostática de pistón-cilindro, capaz de alcanzar 20 kbar, se ha podido preparar (Sr0. 75Ca0. 25)0. 85Nd0. 15·CuO₂, superconductor a 34 K. Trabajar a esas presiones moderadas permite la obtención de cantidades de muestra suficientes para estudios por difracción de neutrones. Se ha refinado la estructura con datos de alta resolución (D2B, ILL) [1] que revelan la presencia de oxígenos axiales que probablemente producen perturbaciones en los planos CuO₂ que son el origen del pequeño volumen Meissner observado en estos materiales. Este trabajo se está desarrollando en el marco de un proyecto financiado por la CICYT [2].

Propiedades electrónicas de los óxidos de cobre

Se han estudiado las excitaciones de carga y spin de baja energía de los óxidos de cobre, a diferentes valores del doping, con un modelo Hubbard bidimensional resuelto por técnicas de campo medio complementadas con la Random Phase Approximation (RPA). Esta aproximación reproduce correctamente las principales características del modelo Hubbard, siendo los resultados obtenidos consistentes con las propiedades de los superconductores de alta T_c.

Se están estudiando también los espectros de los óxidos de cobre obtenidos por fotoemisión, basándonos en el modelo 'Lattice Anderson'. El método de cálculo introduce la correlación de los estados finales y se explican muchas características de los espectros experimentales.

Materiales en comunicaciones

La utilización de nuevos materiales con altas prestaciones es uno de los pilares del avance espectacular de las tecnologías de la información y comunicaciones. El desarrollo de aplicaciones basadas en sus propiedades requiere un profundo conocimiento previo de éstas. En particular, el descubrimiento de superconductividad en óxidos cerámicos multimetálicos a temperaturas superiores a 77 K (superconductores de alta temperatura, SAT) puede permitir del desarrollo práctico de algunas aplicaciones de la superconductividad económicamente inviables con los superconductores clásicos. Sin embargo, la gran complejidad de los SAT y su naturaleza granular dificultan la puesta en marcha de aplicaciones de los mismos de forma inmediata, a pesar del gran esfuerzo investigador que en este campo se está realizando en los países avanzados. En concreto, en nuestro grupo se ha trabajado en la caracterización experimental y modelado fenomenológico de las propiedades electromagnéticas de superconductores de alta temperatura crítica, incidiendo especialmente en las implicaciones de la granularidad, y en el desarrollo de aplicaciones de los mismos en magnetometría y en cintas para el transporte de corriente sin pérdidas. Por otra parte, en relación con las aplicaciones de la superconductividad clásica, se ha trabajado en la implementación en España de los patrones primarios de tensión (efecto Josephson) y resistencia (efecto Hall cuántico), en colaboración con grupos nacionales y extranjeros especializados en metrología eléctrica básica. Por último, también se ha colaborado con otros grupos de investigación en la caracterización electromagnética de materiales de interés tecnológico, como imanes permanentes o aceros estructurales.

líneas de Trabajo Síntesis de materiales de Litio para su uso en reactores de fusión:

El desarrollo de los materiales para revestimiento de reactores de fusión, se basa en la producción de compuestos químicos y cuerpos cerámicos estables bajo las condiciones de trabajo del revestimiento de dichos reactores. Los materiales cerámicos candidatos para dicha aplicación son titanatos, zirconatos, silicatos de Litio. En 1.995 se inicio el proyecto OIEA, "Cerámicas de Litio para Reactores de Fusión". Durante el año 1.995 se desarrollaron tecnologías tendientes a fabricar polvos y piezas de metatitanato de Litio (Li₂TiO₃). Este ha sido sintetizado por reacciones de precipitación, vía sol-gel y reacción sólida. Encontrar las condiciones óptimas de síntesis, con llevó a estudiar el tratamiento térmico que causa la formación del óxido doble. El método sol-gel permitió un control microestructural en la obtención de polvos de alta pureza. Se han caracterizado los polvos de metatitanato de Litio para establecer las características de ellos y su influencia en el comportamiento final del cuerpo cerámico. Para establecer la producción de Tritio a partir de especimenes del cerámico de Litio, estos han sido sometidos a irradiación en el núcleo del reactor. Los especimenes son conformados a partir del polvo fino de metatitanato de Litio por el proceso de extrusión. La forma geométrica del cerámico depende del diseño del blanket. En este caso los especimenes han sido conformados como cilindros de 0,7 mm diámetro promedio. Las piezas cerámicas se someten a irradiación y registro de la liberación de Tritio. Se montó el Laboratorio de Liberación de Tritio y se ha puesto a punto la instrumentación. Se persigue establecer la relación entre microestructura y preparación del cuerpo cerámico para optimizar la liberación de Tritio. La configuración final del revestimiento del reactor de fusión determina fuertemente el mecanismo de extracción del Tritio y su velocidad de liberación. Las formas geométricas afectan la conductividad térmica, tensión térmica, como también la presión del gas de arrastre en la liberación del Tritio. Es por esto que se estudiarán otras formas geométricas, las cuales deberán ser ensayadas en el loop de irradiación que se encuentra en su etapa de diseño.

Obtención de zeolitas de talio:

Las zeolitas de metales alcalinos han sido utilizadas para la fabricación de fuentes de iones. Se requiere, sin embargo, disponer de una zeolita de talio para esta aplicación, debido a que este elemento tiene mayor masa atómica y un primer potencial de ionización relativamente bajo, características importantes en los diagnósticos de plasmas con confinamiento magnético usando haces de iones. La resolución en los diagnósticos se favorece además, si se emplea talio monoisotópico en las fuentes.

El objetivo de este estudio fue desarrollar un procedimiento de síntesis óptimo para la obtención de una zeolita de talio natural en primer lugar y de talio monoisotópico a continuación. Para esto se realizaron experiencias de intercambio iónico a partir de la zeolita comercial X-13 (zeolita de Na) y óxido tálico o carbonato de talio. Este intercambio se realizó en sistema batch controlando la concentración de la solución, tiempos de reacción y temperatura de reacción. Los productos obtenidos han sido caracterizados para determinar la eficiencia del intercambio.

Bibliografía:

• D. Shoenberg, "Superconductivity" (Cambridge Univ. Press, 1952).
• P.G. De Gennes, "Superconductivity of Metals and Alloys" (Addison-Wesley, 1966 and 1989).
• C.G. Kuper, "Introduction to the Theory of Superconductivity" (Clarendon Press, 1968).
• A.C. Rose-Innes and E. H. Rhoderick, "Introduction to Superconductivity" (Pergamon Press, 1968).
• R.D. Parks, Ed., "Superconductivity" (Dekker,1969) Vols 1 y 2.
• M. Tinkham "Introduction to Superconductivity" (Krieger Pub. Co., 1975 y 1980).
• D.H. Douglas, Ed. "Superconductivity in d- and f-Band Metals" (Plenum Press, 1976).
• H.W. Weber, Ed., "Anisotropy Effects in Superconductors" (Plenum Press, 1976).
• R.W. White and T.H. Geballe, "Long Range Order in Solids" (Academic Press, 1979).
• T. VanDuzer and C.W. Turner, "Principles of Superconductive Devices and Circuits" (Elsevier, 1981).
• Ø. Fischer and M.B. Maple, "Superconductivity in Ternary Compounds" (Springer-Verlag 1982), Vols. 1 y 2.
• S.V. Vonsovsky, Y.A. Izyunov, and E.Z. Kurnaev, "Superconductivity in Transition Metals" (Springer-Verlag 1982).
• J.R. Schrieffer,"Theory of Superconductivity" (Addison-Wesley, 1983).
• T.P. Orlando and K.A. Delin, "foundations of Aplied Superconductivity" (Addison-Wesley, 1991).

Autor: Juan Augusto Arauz.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).

• ‹ Anterior
• |
• Siguiente ›