Guía nº 2 de ejercicios de diferenciación

Resolver los siguientes ejercicios

� Ver resolución de los ejercicios al pie de la página

Calcular la longitud de las siguientes curvas:

Problema nº 16

(3·t, 4·t - 1); 0 ≤ t ≤ 1

Problema nº 17

(4 + 2·t, t²/2 + 3); -2 ≤ t ≤ 2

Problema nº 18

x = 2·t + 5, y = t² - 6; 0 ≤ t ≤ 1

Problema nº 19

x = e^t·cos t, y = e^t·sen t; 1 ≤ t ≤ 2

Problema nº 20

x = 2·t + 1, y = t²; 0 ≤ t ≤ 2

Problema nº 21

x^⅔ + y^⅔ = 1; -1 ≤ t ≤ 1

Problema nº 22

• Respuesta: s = 1

Problema nº 23

• Respuesta: s = 2·[2·√6 - √3]

Problema nº 24

Una partícula se mueve según la curva:

X(t) = (cosh t, sinh t, t)

Calcular la distancia recorrida entre t = 0 y t = 1.

Problema nº 25

Calcular el perímetro del dominio plano:

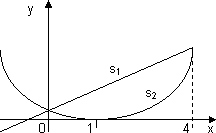
(x - 1)² ≤ 4·y ≤ 1 + 2·x

• Fuente:

"Lecciones de análisis II" del Dr. Alfredo F. Novelli para Análisis Matemático II de UNLu.

Autor: Ricardo Santiago Netto. Argentina

Problemas resueltos:

• Problema nº 22 de funciones de varias variables, longitud de una curva aplicando integrales - TP02

• Problema nº 23 de funciones de varias variables, longitud de una curva aplicando integrales - TP02

• Problema nº 24 de funciones de varias variables, longitud de una curva aplicando integrales - TP02

• Problema nº 25 de funciones de varias variables, longitud de una curva aplicando integrales - TP02