Guía nº 3 de ejercicios de diferenciación
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Fórmulas aplicables:
Dᵤf(X) = ∇f(X)·u
| Dᵤf(x, y) = | ∂f | )·cos x·u + | ∂f | )·cos y·u |
| ∂x | ∂y |
Para:
u = (u₁, u₂)
u₁ = cos x·u
u₂ = cos y·u
o
| Dᵥf(X) = ∇f(X)· | V |
| ||V|| |
Para:
| u = | V |
| ||V|| |
Máxima velocidad de crecimiento de una función f(X) en un punto dado X₀ es:
||∇f(X₀)||
Dirección de máxima velocidad de crecimiento de una función f(X) en un punto dado X₀ es:
∇f(X₀) ⇔ (si: ∇f(X₀) ≠ 0)
Calcular las derivadas direccionales de las siguientes funciones, en los puntos indicados y según las direcciones indicadas:
Problema nº 12
f(x, y) = log y/log x
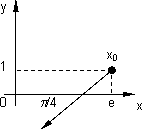
• Respuesta: Dᵤ(e, 1) = (0, 1)·(-½·![]() , -½·
, -½·![]() ) = -½·
) = -½·![]()
Problema nº 13
f(x, y) = (tg x)√y
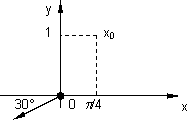
Problema nº 14
f(x, y) = log (1 + √x² + y²)
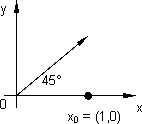
Problema nº 15
f(x, y) = (x² - y²)/x·y
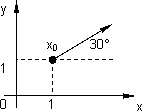
Problema nº 16
f(x, y) = eˣ ⁺ ʸ/(x - y)
Problema nº 17
Dada la función z = x² - x·y + y², hallar, en el punto (1,1):
a) La máxima derivada direccional.
b) La dirección de mayor crecimiento de la función.
c) La dirección de mayor decrecimiento de la función.
d) Las direcciones según las cuales la derivada direccional es nula.
Problema nº 18
Sea f(x, y, z) = x·y + y·z + z·x, hallar, en el punto (1, 2, -1):
a) La dirección en la cual la función crece más rápidamente.
b) La derivada direccional en esa dirección.
c) La mínima derivada direccional.
Problema nº 19
Sea f(x, y, z) = x²·y - ey·z una función que representa la distribución de la temperatura. Calcular en el punto P = (1, 1, 1):
a) La dirección en la cual la temperatura aumenta más rápidamente.
b) La máxima velocidad de crecimiento de la temperatura.
Problema nº 20
Calcular las direcciones según las cuales la función f(x, y) = x² + y³ tiene derivada direccional nula en el punto p = (![]() ,
, ![]() ).
).
Problema nº 21
Demostrar el teorema 1.7.II:
Dᵤ(f + g) = Dᵤf + Dᵤg
Dᵤ(c·f) = c·Dᵤf
Problema nº 22
Demostrar el teorema 1.7.III:
D₋ᵤf = -Dᵤf
• Fuente:
"Lecciones de análisis II" del Dr. Alfredo F. Novelli para Análisis Matemático II de UNLu.
Autor: Ricardo Santiago Netto. Argentina