Gunía n° 10 de ejercicios de operaciones con números reales

Resolver los siguientes ejercicios

Hallar los valores de x que verifiquen, aplicando definición y propiedades del módulo:

Problemas de potenciación, radicación y valor absoluto con números reales

Resolver:

Problemas de potenciación y radicación con números reales

Hallar los valores de x que verifiquen:

Problemas de potenciación y radicación con números reales

Racionalizar los denominadores de las siguientes fracciones:

Problemas de potenciación y radicación con números reales

Calcular:

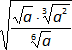Problemas de potenciación y radicación con números reales

Autor: Ricardo Santiago Netto (Administrador de Fisicanet)

San Martín. Buenos Aires. Argentina.