Guía nº 2 de ejercicios de estática
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
Dos pesos de 10 N están suspendidos en los extremos de una cuerda que pasa por una polea ligera sin rozamiento. La polea está sujeta a una cadena que cuelga del techo. Determinar:
a) La tensión de la cuerda.
b) La tensión de la cadena.
• Respuesta:
a) T₁ = T₂ = 10 N;
b) T = 20 N
Problema nº 2
En un taller mecánico, se levanta el motor de un automóvil, cuyo peso es de 350 kgf, por medio de un aparejo diferencial. Si los radios de las poleas son R = 15 cm y r = 12 cm, ¿cuál es la fuerza que equilibra ese peso?
• Respuesta: F = 343,2 N
Problema nº 3
Los radios de un aparejo diferencial son R = 20 cm y r = 15 cm. Si se aplica una fuerza de 80 kgf, ¿cuál es el peso del cuerpo que la equilibra?
• Respuesta: P = 6.276,3 N
Problema nº 4
En una palanca de 2° genero, tiene un brazo de potencia Bp = 1,20 m y un brazo de resistencia Br = 8 cm. Entonces la multiplicación de la palanca es:
a) 6
b) 12
c) 15
d) 20
• Respuesta: M = 15
Problema nº 5
Calcular a que distancia de una potencia de 60 kgf estará apoyada una barra rígida de hierro, para equilibrar un cajón de 300 kgf que está a 0,75 m del apoyo.
• Respuesta: BF = 3,75 m
Problema nº 6
Calcular la potencia que es necesario aplicar a una polea fija, para levantar un peso de 80 kgf.
• Respuesta: Q = 784,5 N
Problema nº 7
¿Qué potencia se aplicará para equilibrar una resistencia de 90 kgf, mediante una polea móvil?
• Respuesta: Q = 441,3 N
Problema nº 8
Sobre un cilindro de 30 cm de diámetro (que puede girar en torno a un eje), está arrollada una soga. Si se le aplica una fuerza (peso) de 1,8 kgf, ¿cuál es el valor del momento que hace girar el cilindro?
• Respuesta: MP = 2,65 N·m
Problema nº 9
Dos bloques unidos por cables de acero se encuentran en posición de equilibrio, tal como muestra la figura. Si el ángulo α = 45° y las tensiones T₁ y T₂ valen 405 kgf y 980 kgf respectivamente, calcular los valores de m₁ y m₂.
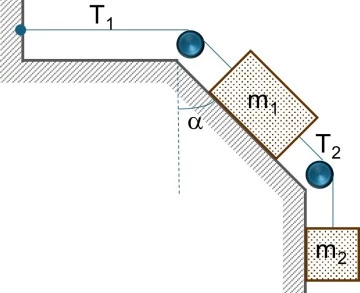
• Respuesta: m₁ = 813,17 kg; m₂ = 405 kg
Problema nº 10
En el plano inclinado como el de la figura, calcular el valor de m₂ y T, si m₁ pesa 5 kgf, α = 30° y β = 60°.
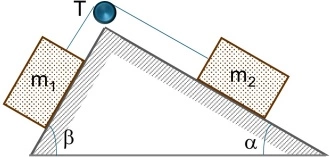
• Respuesta: m₂ = 8,66 kg; T = 4,33 kgf
Bibliografía:
"Física". Hernán Miguel y Marcelo C. Cánepa. 1983. Argentina.
Autor: Ricardo Santiago Netto. Argentina
Problemas resueltos:
Problemas de estática resueltos y fáciles. ¿Cómo resolver problemas de estática?