Guía nº 5 de ejercicios resueltos de estática
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
Un bloque es arrastrado hacia la derecha a velocidad constante por una fuerza de 10 N que actúa formando un ángulo de 30° sobre la horizontal. El coeficiente de rozamiento entre el bloque y le superficie es de 0,50. ¿Cuál es el peso del bloque?
• Respuesta: P = 22,32 N
Problema nº 2
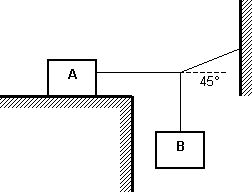
El bloque A de la figura pesa 100 N, el coeficiente de rozamiento entre el bloque y la superficie es de 0,30. El bloque B pesa 20 N y el sistema está en equilibrio. Determinar:
a) El valor de la fuerza de rozamiento ejercida sobre el bloque A.
b) El peso máximo que puede tener el bloque B para que el sistema permanezca en equilibrio.
• Respuesta:
a) TCx = 20 N;
b) FR = 20 N
Problema nº 3
Según el caso de la figura determinar el peso del cuerpo suspendido si la tensión de la cuerda diagonal es de 20 N.
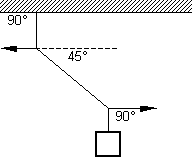
• Respuesta: P = 14,2 N
Problema nº 4
Hay que bajar una caja fuerte de 2.000 N a velocidad constante por una rampa de 4 m de longitud, desde un camión de 2 m de altura. El coeficiente de rozamiento entre la caja fuerte y la rampa es de 0,30. Determinar:
a) ¿Hay que empujar o frenar la caja?
b) ¿Qué fuerza paralela a la rampa es necesaria?
• Respuesta:
a) Frenar la caja;
b) F = 480 N
Problema nº 5
Calcula la fuerza de F₁, F₂ y F₃ para que la barra este en equilibrio.
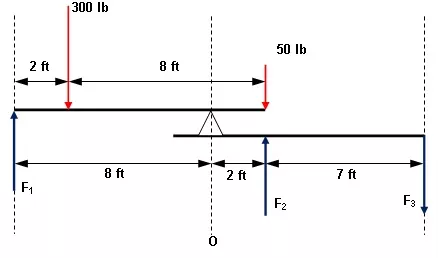
• Respuesta: F₁ = -212,5 lb; F₂ = 176,8 lb; F₃ = -39,3 lb
Problema nº 6
Una cuerda rodea 1/6 del perímetro de una polea móvil que soporta un peso P = 120 N. ¿Qué esfuerzo hay que aplicar al extremo de la cuerda para mantener el equilibrio?
• Respuesta: 120 N
Problema nº 7
Hallar la resultante del sistema de fuerzas concurrentes que muestra la figura. Siendo F₁ = 5 kgf, F₂ = 10 kgf, F₃ = 4 kgf y α = 30°.
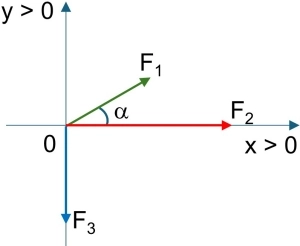
• Respuesta: R = 14,4 kgf
Problema nº 8
Una polea móvil soporta un peso de 80 N. El extremo libre de la cuerda está arrollado al cilindro de un torno de 0,20 m de radio. ¿Qué esfuerzo debe aplicarse a la manivela del torno cuya longitud es 0,50 m para equilibrar el sistema?
• Respuesta: 16 N
Problema nº 9
Se tiene un aparejo diferencial cuyos radios son: R = 25 cm y r = 20 cm. ¿Qué esfuerzo debe aplicarse, teóricamente, para equilibrar un peso de 2.000 N?
• Respuesta: 200 N
Problema nº 10
Hallar la resultante del sistema de fuerzas concurrentes que muestra la figura.
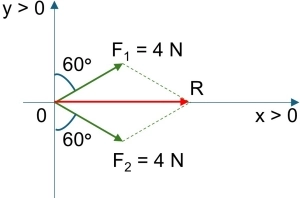
• Respuesta: R = 6,92 N
Responder el siguiente cuestionario
Pregunta nº 1
Si se tira de los extremos de una cuerda en equilibrio con dos fuerzas iguales y de sentido opuesto, ¿por qué la tensión total en la cuerda es cero?
Pregunta nº 2
Un caballo está enganchado a un carro. Como el carro tira del caballo hacia atrás con la misma fuerza que éste tira del carro, ¿por qué no permanece el carro en equilibrio, independientemente de lo que tire el caballo?
Pregunta nº 3
¿Cómo se puede empujar hacia abajo el pedal de una bicicleta y lograr que la bicicleta se mueva hacia adelante?
Pregunta nº 4
Para empujar una caja hacia arriba por una rampa, ¿es mejor empujarla horizontal o paralelamente a la rampa?
Pregunta nº 5
¿De qué depende el coeficiente de rozamiento entre dos superficies?
Pregunta nº 6
¿Puede el coeficiente de rozamiento ser mayor que la unidad? En caso afirmativo dé un ejemplo; de lo contrario explique por qué no puede serlo.
Bibliografía:
"Física". Hernán Miguel y Marcelo C. Cánepa. 1983. Argentina.
Autor: Ricardo Santiago Netto. Argentina