Guía nº 3 de ejercicios resueltos de plano inclinado
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
En todos los casos usar g = 10 m/s²
Problema nº 1
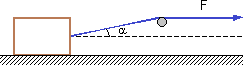
Una caja que pesa 200 N es arrastrada por una cuerda que forma un ángulo α con la horizontal, según muestra la figura. El coeficiente de rozamiento estático entre la caja y el suelo es μₑ = 0,6. Si la caja se encuentra inicialmente en reposo, calcular la fuerza mínima para ponerla en movimiento. Resolver el problema para:
a) α = 30°.
b) α = 0°.
F = 102,91 N; F = 120 N
Problema nº 2
Calcular la fuerza máxima en la dirección de la base del plano que hay que ejercer, para que el cuerpo no se mueva, así como la fuerza mínima.
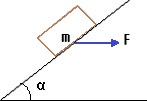
Datos:
μ = 0,3
m = 5 kg
α = 30°
F = 53,1 N; F = 11,8 N
Problema nº 3
Un bloque se encuentra en reposo sobre un plano inclinado que forma un ángulo α con la horizontal. Se encuentra experimentalmente que si se incrementa el ángulo de inclinación, el bloque comienza a deslizarse a partir de un ángulo αc. El coeficiente de rozamiento estático es μₑ = 0,4. Calcular el ángulo αc.
α = 21,8°
Problema nº 4
La cuerda se rompe para una tensión de 1.000 N. Calcular la fuerza con la que hay que tirar de m₁, para que se rompa la cuerda si μ = 0,1 entre los dos cuerpos, y μ = 0,2 entre m₁ y la superficie.
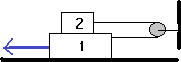
Datos:
m₁ = 10 kg
m₂ = 1 kg
F = 1.023 N
Problema nº 5
Calcular la aceleración que tiene el bloque en un plano inclinado de α = 30° y la reacción del vínculo si m = 4 kg.
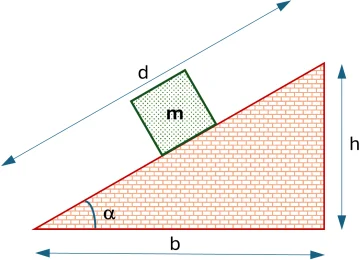
Figura 1
• Respuesta: a = 4,9 m/s²; N = 3,46 kgf
Problema nº 6
Calcular la fuerza necesaria para hacer subir una masa m por un plano inclinado que forma un ángulo α con la vertical, con una aceleración a.
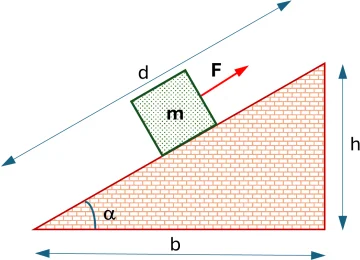
Figura 2
• Respuesta: F = m·(a + g·cos α)
Problema nº 7
Calcular con qué aceleración y hacia dónde se mueve el bloque de la "figura 2" si α = 30° y:
a) m = 8 kg; F = 100 N
b) m = 8 kg; F = 4 kgf
c) m = 6 kg; F = 24 N
• Respuesta:
a) a = 7,6 m/s²; hacia arriba;
b) a = 0;
c) a = -0,9 m/s²; hacia abajo
Problema nº 8
¿Cuál es la fuerza mínima necesaria para subir un peso de 100 kgf a una altura h de 1,5 metros por el plano inclinado de la "figura 1" de 3 metros de longitud d?
• Respuesta: F = 50 kgf
Problema nº 9
Se necesita subir una carga de 100 kgf de peso a una altura de 20 metros. ¿Cuál es la longitud mínima que puede tener el plano inclinado de la "figura 1" si se dispone de una fuerza de 40 kgf?
• Respuesta: d = 50 m
Problema nº 10
Calcular la velocidad que tiene el bloque al llegar a la base de un plano inclinado de la "figura 1" de α = 30°, α = 45°, α = 20°; si parte del reposo desde una altura h = 10 m.
• Respuesta: v₂ = 14 m/s
Responder el siguiente cuestionario
Pregunta nº 1
¿Qué tipo de fuerzas de rozamiento conoce?
Pregunta nº 2
¿Cómo se puede reducir el rozamiento?
Pregunta nº 3
Indicar en que caso el rozamiento ayuda o provoca inconvenientes:
a) Al caminar.
b) En los mecanismos de un motor.
c) En los frenos de una bicicleta.
d) En los rodamientos de las ruedas de la bicicleta.
Pregunta nº 4
¿De qué depende el rozamiento?
Bibliografía:
"Física". Hernán Miguel y Marcelo C. Cánepa. 1983. Argentina.
Autor: Ricardo Santiago Netto. Argentina
Problemas resueltos:
Dinámica práctica