Guía nº 3 de ejercicios resueltos de ecuaciones de primer grado

Resolver los siguientes ejercicios

� Ver resolución de los ejercicios al pie de la página

Problema nº 1

Resolver las siguientes ecuaciones de primer grado, hallar el valor de "x":

a) 5·(x - 7) + 7·(x + 7) = 42

• Respuesta: x = 7/3

b) (8 - x)·(x - 3) = (6 - x)·(x - 5)

• Respuesta: No tiene solución

c)

• Respuesta: x = -3

d)

• Respuesta: x = 5/22

e)

• Respuesta: x = 1

f)

• Respuesta: y = 6

g)

• Respuesta: x = 4/3

h)

• Respuesta: x = 17/4

i)

• Respuesta: x = 3

j)

• Respuesta: x = 2

k)

• Respuesta: x = 5

l)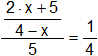

• Respuesta: x = 0

Problema nº 2

Resolver las siguientes ecuaciones de primer grado, hallar el valor de "x":

a)

• Respuesta: x = -a + b

b)

• Respuesta: x = m/n

c)

• Respuesta:

d)

• Respuesta: x = a

e)

• Respuesta: x = -8/3

f)

• Respuesta: x = 5

g)

• Respuesta: x = 6/5

h)

• Respuesta: x = ⅔

i) n²·(a·x + b) = a·n²·x

• Respuesta: no es una ecuación

j)

• Respuesta: x = a² + 1

k)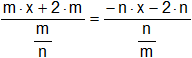

• Respuesta: n = -m

Autor: Ricardo Santiago Netto. Argentina

• ‹ Anterior
• |
• Siguiente ›

Hallar el valor de "x".