Guía nº 9 de ejercicios resueltos de operaciones con raíces y racionalización
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
Efectuar las siguientes operaciones:
a) √2·√8 =
b)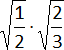 
=
c)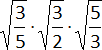 
=
d) ∛60·∛90·∛5 =
e) √√a + √b·√√a - √b =
f) ∛14·a·b²÷∜7·a³·b² =
g)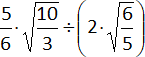 
=
h) √x·y³÷∛x·y⁴ =
i)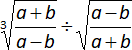 
=
j) 
=
k) 
=
l)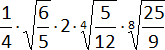 
=
m)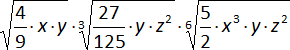 
=
n) 
=
o) 
=
p)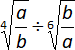 
=
q)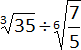 
=
r) 
=
• Respuesta:
a) 4;
b) 
;
c) 
;
d) 30;
e) √a - b;
f) 
;
g) 25/36;
h) 
;
i)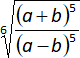 
;
j) 
;
k) 
;
l) ½;
m)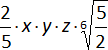 
;
n) 2·√3;
o)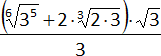 
;
p)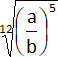 
;
q) 
;
r) 
Problema nº 2
Racionalizar los denominadores de las siguientes fracciones:
| a) | 2 | = |
| √2 |
| b) | 1 | = |
| √3 |
| c) | 2 | = |
| √3³ |
| d) | 1 | = |
| ∛2 |
| e) | 2·a | = |
| ∛7 |
| f) | 3 | = |
| 4·√2·y |
| g) | 1 | = |
| √1/x |
| h) | 1 | = |
| ∛1/a |
| i) | 2 + ∛4 | = |
| 3·∛4 |
| j) | ∜8·a | = |
| √2·√2·a |
| k) | 1 | = |
| 2·√2·a·∛2·b |
| l) | 1 | = |
| 2 - √3 |
| m) | 1 | = |
| √5 - 2 |
| n) | 1 | = |
| √2 + √3 |
| o) | 3·√5 - √3 | = |
| 4·√5 + 5·√3 |
| p) | √a² + b² - √a² - b² | = |
| √a² + b² + √a² - b² |
| q) | a·√2 - 2·√a | = |
| √a + √2 |
| r) | 1 | = |
| √2 - √3 |
| s) | 3 | = |
| √11 + 2·√10 |
| t) | √7 | = |
| √x + √x² - y |
| u) | 1 - 2·√2 | = |
| 2·√2 - √7 + 2·√2 |
| v) | 1 | = |
| √a + √b + √c |
w) 
=
x) 
=
y) 
=
z)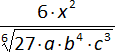 
=
• Respuesta:
a) √2;
b) ⅓·√3;
c) ⅑·2·√3;
d) ½·∛4;
e) ⅐·2·a·∛49;
f) 3·√2·y÷8·y;
g) √x;
h) ∛a;
i) ⅓·∛2 + 1;
j) ½·∜4·√2;
k) √2·a·∛4·b²÷8·a·b;
l) 2 + √3;
m) √5 + 2;
n) √3 - √2;
o) ⅕·75 - 19·√15;
p) a² - √a⁴ - b⁴÷b²;
q) (a·√2·a - 4·a + 2·√2·a)÷(a - 2);
r) (√2 - √3)·(2 + √3);
s) (√11 + 2·√10)·(11 - 2·√10)÷27;
t) -√7·(√x + √x² - y)·(x - √x² - y)÷y;
u) 2·√2 + √7 + 2·√2;
v) (√a - √b + √c)·(a - b - c + 2·√b·c)÷(a² - 2·a·b - 2·a·c + b² + c² - 2·b·c);
w) 
;
x) 
;
y) 
;
z)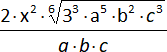 
Autor: Ricardo Santiago Netto. Argentina